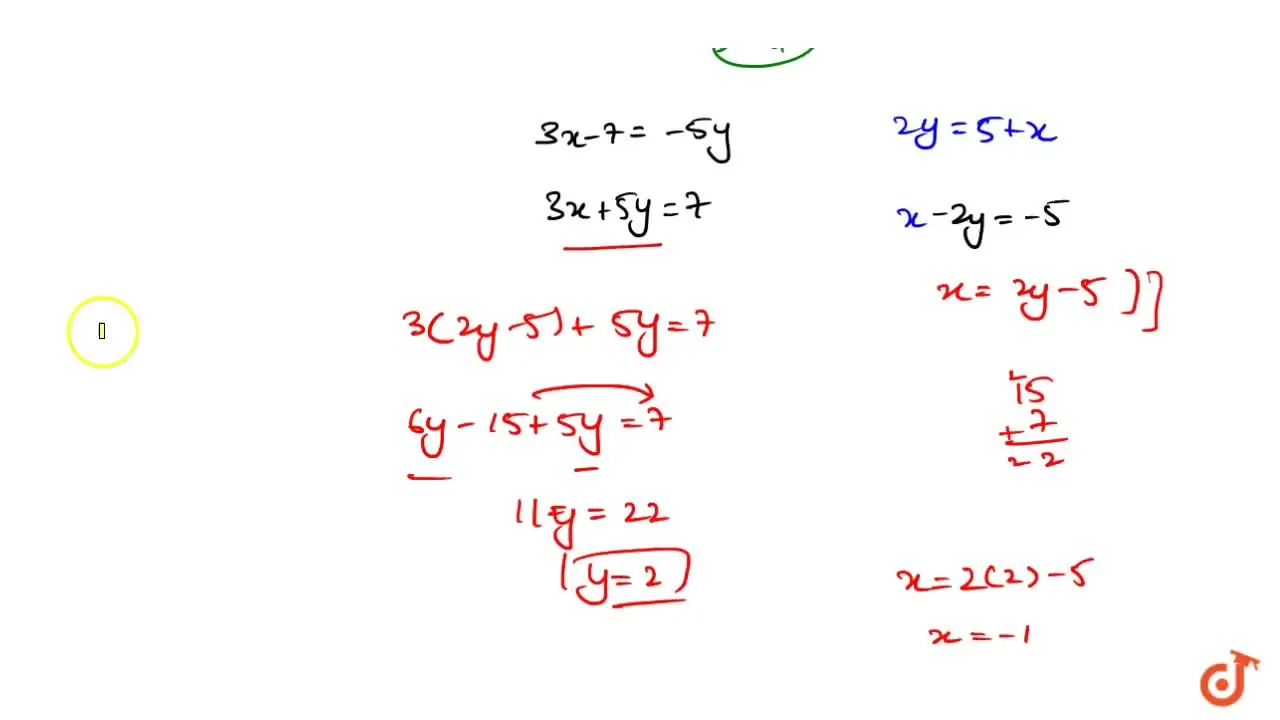Find the real values of xandy, if (3x−7)+2iy=−5y+(5+x)i
Video Solution
Text Solution
We have given, (3x−7)+2iy=−5y+(5+x)i
Compare real and imaginary parts
3x−7=−5yand
2y=5+x
⇒y=5+x2
So we have3x−7=−(52)(5+x)
6x−14=−25−5x
⇒11x=−11
⇒x=−1
so y=5+x2=(5−12)=2
Hence the values of x,y are -1,2
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find the real values of x and y,if (3x−7)+2iy=−5y+(5+x)i
View SolutionFind the real values of xandy, if (3x−7)+2iy=−5y+(5+x)i
View SolutionFind the real values of x and y if (i)(3x−7)+2iy=−5y+(5+x)i (ii)(x+iy)(2−3i)=(4+i)
View SolutionFind the real values of x and y, if:(x+iy)(2−3i)=4+i
View SolutionFind the real values of x and y, if:(1+i)(x+iy)=2−5i
View SolutionFind the real values of x and y, if:(3x−2iy)(2+i)2=10(1+i)
View SolutionFind the value of x and y if (i) 3x+(2x−y)i=6−3i (ii) 3x+5yi=5i
View SolutionFind the values of xandy if [x+10y2+2y0−4]=[3x+430y2−5y]
View SolutionFind the real value of xandy if (1+i)x−2i3+i+(2−3i)y+i3−i=i
View SolutionFind the values of x and y from the following : (i) (3x−7)+2iy=−5y+(5+x)i (ii) 2xi+12=3y−6i (iii)z=x+iyandi(z+2)+1=0 (iv)(1+i)x−2i3+i+(2−3i)y+i3−i=i (v) (3x−2iy)(2+i)2=10(1+i)
View Solution