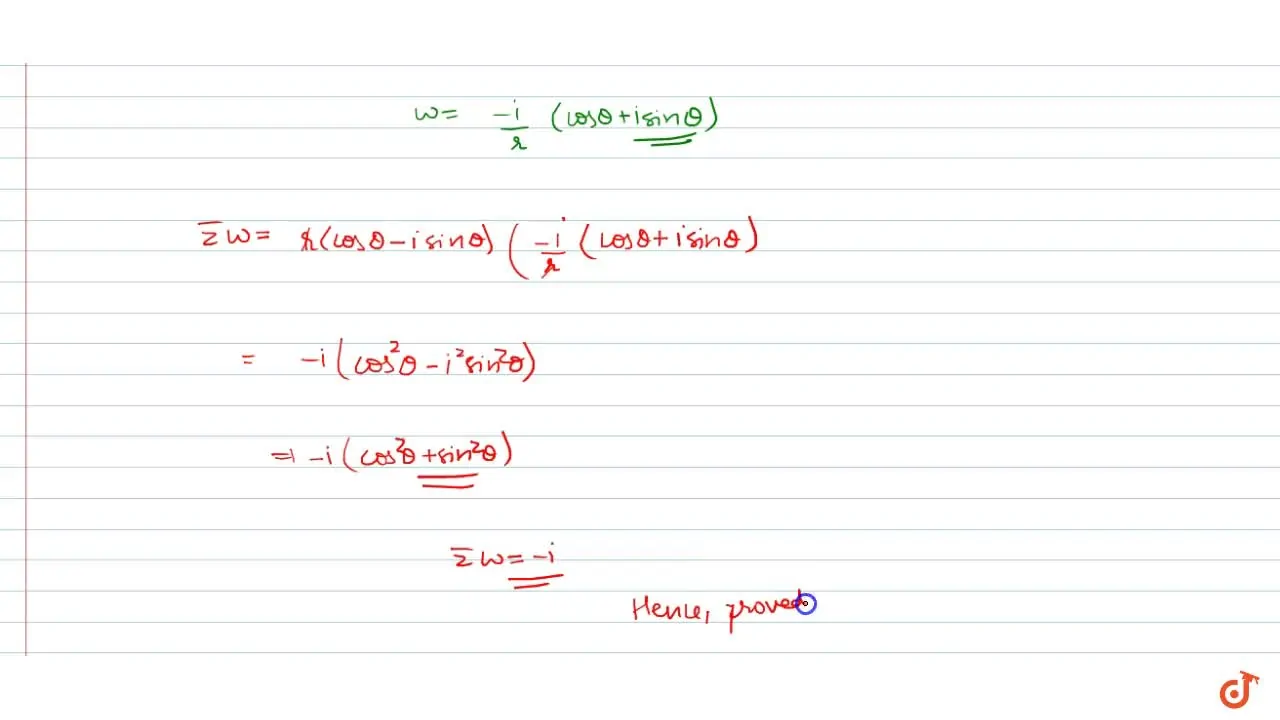If zandw are two complex number such that |zw|=1andarg(z)–arg(w)=π2, then show that ¯zw=−i.
Let
z=r!eiθandw=r∘eiϕ
⇒¯z=r1eiθ
Given,
⇒∣∣r1eiθ⋅r2eiϕ∣∣=1
⇒r1r2=1 .........(i)
and arg(z)−arg(w)=π2
⇒θ−ϕ=π2 ......(ii)
now,
¯zw=r1e−iθ⋅r2eiϕ=r1r2e−i(θ−ϕ)
=1⋅eπ2 [from eqs. (i) and (ii) ]
=cosπ2−isinπ2
⇒¯zw=−i
Related Playlists
Similar Questions
If zandw are two complex number such that |zw|=1andarg(z)–arg(w)=π2, then show that ¯zw=−i.
View SolutionLet Z and w be two complex number such that |zw|=1 and arg(z)−arg(w)=π/2 then
View SolutionIf z and w are two non - zero complex numbers such that |zw|=1andarg(z)−arg(w)=π2, then the value of 5i¯zw is equal to
View SolutionIf z ans w are two non-zero complex numbers such that |zw|=1 and arg (z) = arg (w) =π2,¯zw is equal to
View SolutionLet zandw be two nonzero complex numbers such that |z|=|w|andarg(z)+arg(w)=π. Then prove that z=−¯¯¯w.
View SolutionIf z1andz2 are two complex numbers such that |z1|=|z2|andarg(z1)+arg(z2)=π , then show that z1,=−(z)2.
View Solutionz1thez2are two complex numbers such that|z1|=|z2|. "and"
arg (z1)+arg(z2=π, then show that z1=−¯z2.View SolutionLet zandw be two non-zero complex number such that |z|=|w| and arg(z)+arg(w)=π , then z equals. w (b) −w (c) w (d) −w
View SolutionLet a complex number be w=1−√3I, Let another complex number z be such that |z w|=1 and arg(z)-arg (w) =π2. Then the area of the triangle with vertices origin, z and w is equal to :
View SolutionLet z1 and z2 be two complex numbers such that |z1|=|z2|and arg(z1)+arg(z2)=π then which of the following is correct?
View Solution