If the perimeter of a rectangular flower bed is 30 feet, and its area is 44 square feet, what is the length of each of its shorter sides?
The correct Answer is:4 feet
To solve the problem step by step, we will use the formulas for the perimeter and area of a rectangle.
1. Understand the Problem: We need to find the length of the shorter side of a rectangular flower bed, given its perimeter and area.
2. Write the Formulas:
- The formula for the perimeter P of a rectangle is:
P=2(l+b)
where l is the length and b is the breadth.
- The formula for the area A of a rectangle is:
A=l×b
3. Set Up the Equations:
- Given that the perimeter is 30 feet:
2(l+b)=30
Dividing both sides by 2:
l+b=15(Equation 1)
- Given that the area is 44 square feet:
l×b=44(Equation 2)
4. Express One Variable in Terms of the Other:
- From Equation 1, we can express l in terms of b:
l=15−b
5. Substitute into the Area Equation:
- Substitute l in Equation 2:
(15−b)×b=44
Expanding this gives:
15b−b2=44
Rearranging it to standard quadratic form:
b2−15b+44=0(Equation 3)
6. Factor the Quadratic Equation:
- We need to factor Equation 3. We look for two numbers that multiply to 44 and add to -15. The numbers are -11 and -4:
(b−11)(b−4)=0
7. Solve for b:
- Setting each factor to zero gives:
b−11=0⇒b=11
b−4=0⇒b=4
8. Find Corresponding Lengths:
- If b=11, then:
l=15−11=4
- If b=4, then:
l=15−4=11
9. Identify the Shorter Side:
- The lengths are 11 feet and 4 feet. Therefore, the length of the shorter side is:
Shorter side=4 feet
Final Answer:
The length of each of its shorter sides is 4 feet.
- The formula for the perimeter P of a rectangle is:
P=2(l+b)
where l is the length and b is the breadth.
- The formula for the area A of a rectangle is:
A=l×b
- Given that the perimeter is 30 feet:
2(l+b)=30
Dividing both sides by 2:
l+b=15(Equation 1)
- Given that the area is 44 square feet:
l×b=44(Equation 2)
- From Equation 1, we can express l in terms of b:
l=15−b
- Substitute l in Equation 2:
(15−b)×b=44
Expanding this gives:
15b−b2=44
Rearranging it to standard quadratic form:
b2−15b+44=0(Equation 3)
- We need to factor Equation 3. We look for two numbers that multiply to 44 and add to -15. The numbers are -11 and -4:
(b−11)(b−4)=0
- Setting each factor to zero gives:
b−11=0⇒b=11
b−4=0⇒b=4
- If b=11, then:
l=15−11=4
- If b=4, then:
l=15−4=11
- The lengths are 11 feet and 4 feet. Therefore, the length of the shorter side is:
Shorter side=4 feet
The length of each of its shorter sides is 4 feet.
Similar Questions
Knowledge Check
The perimeter of a rectangular field is 216 metres and its breadth is 40 metres . Find the length and area of the rectangle.
A=4720m2.B=3720m2.C=2920m2.D=2720m2.The perimeter of a rectangular field is 92m. If its length is 26m , find its breadth and area.
A20m;520m2B10m;510m2C20m;420m2D25m;580m2If the perimeter of a square is 50 cm, then its side is
A200 cmB150 cmC25 cmD12.5 cm
The perimeter of a rectangular plot of land is 240 m and its length is 63 m . Find the breadth and area of the plot.
View SolutionThe perimeter of a rectangular sheet is 40 feet. If the length of the sheet is three times the breadth, find its dimensions.
View SolutionIf the perimeter of a square is 36 cm, then its area is
View SolutionThe top surface of a rectangular table has an area of 100 square feet and a width of 5 feet. What is the length, in feet, of the surface?
View SolutionWhat is the area, in square feet, of the figure below?
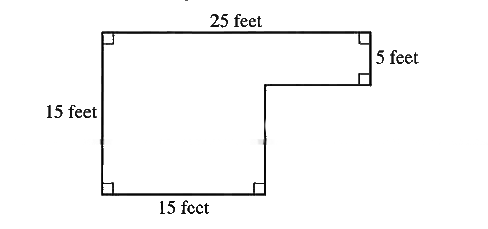
View Solution
