A rectangular swimming pool has a length of 30 meters, a width of 10 meters, and an average depth of 2 meters. If a hose can fill the pool at a rate of 0.5 cubic meters per minute, how many hours will it take the hose to fill the pool?
The correct Answer is:20 hours
To solve the problem step by step, let's follow the outlined process:
Step 1: Calculate the volume of the swimming pool
The volume V of a rectangular swimming pool can be calculated using the formula:
V=length×width×depth
Given:
- Length = 30 meters
- Width = 10 meters
- Depth = 2 meters
Substituting the values into the formula:
V=30m×10m×2m=600cubic meters
Step 2: Determine the rate at which the hose fills the pool
The hose fills the pool at a rate of:
Rate=0.5cubic meters per minute
Step 3: Calculate the time taken to fill the pool in minutes
To find the total time T in minutes to fill the pool, we use the formula:
T=Volume of the poolRate of filling
Substituting the known values:
T=600cubic meters0.5cubic meters per minute=1200minutes
Step 4: Convert the time from minutes to hours
To convert minutes into hours, we use the conversion:
Hours=Minutes60
Substituting the value we calculated:
Hours=1200minutes60=20hours
Final Answer
It will take the hose 20 hours to fill the swimming pool.
---
The volume V of a rectangular swimming pool can be calculated using the formula:
V=length×width×depth
Given:
- Length = 30 meters
- Width = 10 meters
- Depth = 2 meters
V=30m×10m×2m=600cubic meters
The hose fills the pool at a rate of:
Rate=0.5cubic meters per minute
To find the total time T in minutes to fill the pool, we use the formula:
T=Volume of the poolRate of filling
Substituting the known values:
T=600cubic meters0.5cubic meters per minute=1200minutes
To convert minutes into hours, we use the conversion:
Hours=Minutes60
Substituting the value we calculated:
Hours=1200minutes60=20hours
It will take the hose 20 hours to fill the swimming pool.
Similar Questions
A cylindrical water tank has a diameter of 14 meters and a height of 20 meters. A water truck can fill π cubic meters of the tank every minute. How long will take the water truck to fill water tank from empty to half full?
View SolutionTo fill swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool
View Solution
Knowledge Check
The plans for a diving pool call for a rectanglular prism that has a length of 30 meters, a width of 25 meters, and a depth of 5 meters. If the plans are changed to increase both the length and the width of the pool by 10%, what will be the increase, to the nearest 1%, in the volume of the pool?
A0.1B0.17C0.2D0.21If a rectangular swimming pool has a volume of 16,500 cubic feet, a uniform depth of 10 feet, and a length of 75 feet, what is the width of the pool, in feet?
A22B26C32D110Hose A can fill a tank in 5 minutes, and Hose B can fill the tank the same tank in 6 minutes. How many tanks would Hose B fill in the time Hose A fills 6 tanks ?
A3B4C5D5.5
Randy can run π meters every 2 seconds. If the circular track has a radius of 75 meters, how many minutes does it take Randy to run twice around the track?
View SolutionA partially filled pool contains 600 gallons of water. A hose is turned on, and water flows into the pool at the rate of 8 gallons per minute. How many gallons of water will be in the pool after 70 minutes?
View SolutionTwo hoses attached to separate water sources are available to fill a cyindrical swimming pool. If both hoses are used , the time it will take to fill the pool can be represented by the following equation : 1T1+1T2=1Tc, where T1andT2 represent the time needed for hoses 1 and 2 , respectively , to fill the pool on their own , and Tc represents the time needed for hoses 1 and 2 to fill the pool working together . IF hose 1 alone can fill the pool in exactly 20 minutes and hose 2 alone can fill the pool in exactly 60 minutes , how many minutes will it take to fill the pool if both hoses work simultaneously ?
View SolutionThe length, width and depth of a rectangular box are 6 feet, 5 feet and 7 feet, respectively. A hose supplies water at a rate of 6 cubic feet per minute. How much time in minutes would it take to fill a conical box whose volume is three times the volume of the rectangle box?
View SolutionA square field measures 10 meters by 10 meters. Ten students each mark off a randomly selected region of the field, each region is square and has side lengths of 1 meter, and no two regions overlap. The students count the earthworms contained in the soil to a depth of 5 centimeters beneath the ground’s surface in each region. The results are shown in the table below.
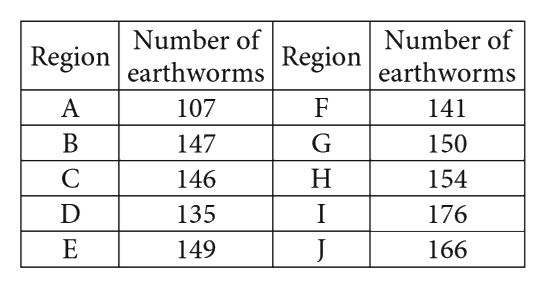
Which of the following is a reasonable approximation of the number of earthworms to a depth of 5 centimeters beneath the ground’s surface in the entire field?
View Solution
