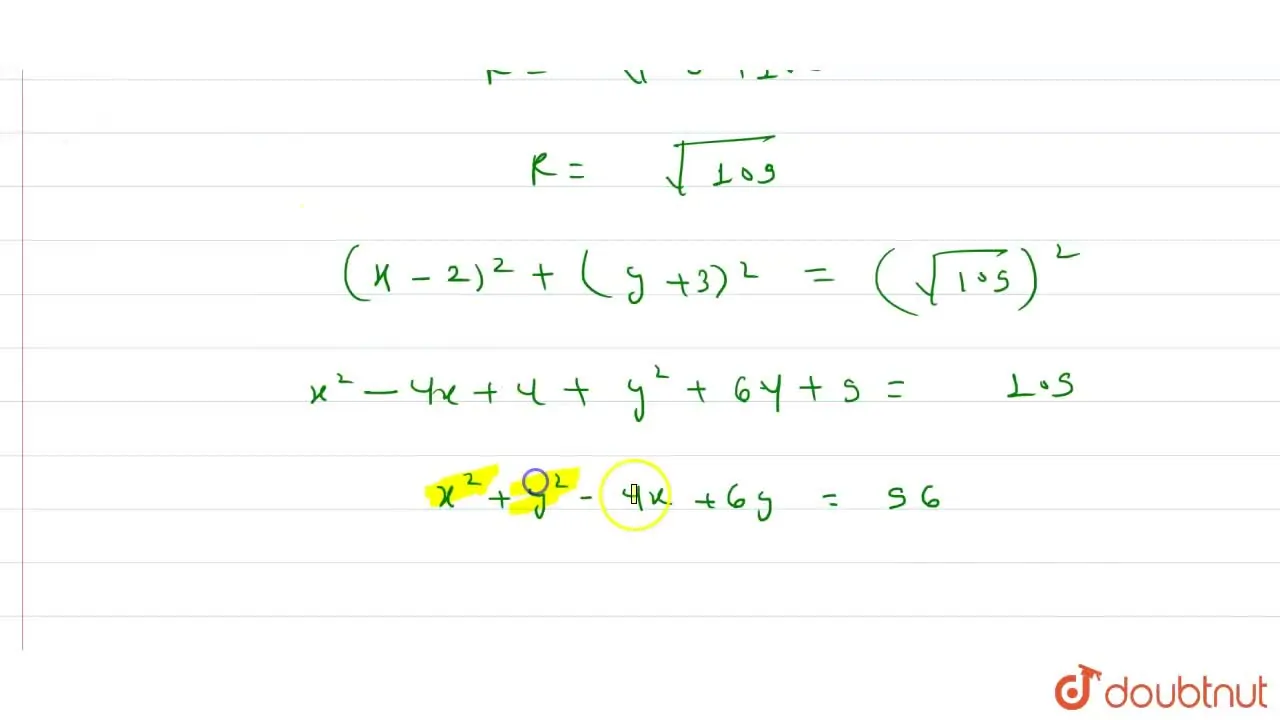Find the equation of the circle which passes through the point of intersection of the lines and whose centre .
Let P be the point of intersection of the lines AB and LM whose equations are respectively
and
Solving (1) and (2) we get
So coordinates of P are Let be the centre of the circle Since the circle passes through P therefore
CP = radius =
⇒radius=
Hence the equation of the required circle is
Related Playlists
Similar Questions
Find the equation of the circle which passes through the point of intersection of the lines 3x−2y−1=0and4x+y−27=0 and whose centre (2,−3) .
View SolutionFind the equation to the circle which passes through the point of intersection of 3x−2y−1=0and4x+y−27=0 and whose centre is (2, 3)
View SolutionFind the equation of a line passing through the point of intersection of the lines x+3y+1=0 and 2x−y+3=0 and parallel to the line 3x−2y+1=0.
View SolutionFind the equation of the line which passes through the point of intersection of the lines 2x-y+5=0 and 5x+3y-4 =0 and is perpendicular to the line x-3y+21 =0
View SolutionFind the equation of the circle passing through the point of intersection of the lines x+3y=0 and 2x−7y=0 and whose centre is the point of intersection of the lines x+y+1=0 and x−2y+4=0.
View SolutionFind the equation of the line which passes through the point of intersection of the lines 2x-y+5=0 and 5x+3y-4 =0 and is perpendicular to the line x-3y+21 =0
View SolutionFind the equation of the line which passes through the point of intersection of the lines x + 2y - 3 = 0 and 4x - y + 7 = 0 and is parallel to the line y - x + 10 = 0.
View SolutionFind the equation of a line which passes through the point (1,1) and through the intersection of lines x+y−1=0 and 3x+2y+1=0.
View SolutionFind the equations of the line passing through the point of intersection of the lines 3x−2y+4=0, 2x−5y=1 and whose distance from (2,–1) is 2.
View SolutionFind the equation of a line which passes through the intersection of the lines 3x+y−2=0 and x−y+1=0 and parallel to Y-axis.
View Solution