जब त्रिज्या r1 व r2 ( जहाँ r2>r1 ) के साबुन के दो बुलबुले मिलते हैं, तो उनके उभयनिष्ठ तल की वक्रता त्रिज्या होगी :
12(r2+r1)
√r21r22
r1r2r2−r1
r2+r1.
4Tr1−4Tr2=4TR या 1R=1r1−1r2 या R=r1r2r2−r1
Topper's Solved these Questions
- तरल के यान्त्रिक गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - तरल के यान्त्रिक गुणEXERCISE - NCERT पाठ्य पुस्तक के प्रश्नोत्तर
48 Videos
- तरंगे BOOK - SHIVLAAL PUBLICATIONCHAPTER - तरंगे EXERCISE - वस्तुनिष्ठ प्रश्न
202 Videos
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - वस्तुनिष्ठ प्रश्न
79 Videos
Similar Questions
स्पष्ट कीजिये क्यों -
मस्तिष्क की अपेक्षा मानव का पैरो पर रक्त चाप अधिक होता है |
View Solution20 मीटर लम्बाई की एकसमान डोरी को एक दृढ़ आधार से लटकाया गया है। इसके निचले सिरों पर एक तरंग स्पन्द प्रवेश करती है। इसे ऊपर आधार तक पहुँचने में लगा समय होगा(g=10 मी/से2) :
View Solutionसरल आवर्त गति करते हुए एक कण के सम्बन्ध में असत्य कथन है :
View Solution(r_(3)+r_(1))(r_(3)+r_(2))sin C=2r_(3)sqrt(r_(2)r_(3)+r_(3)r_(1)+r_(1)r_(2))
View SolutionValue of 1r21+1r22+1r23+1r2 is :
View Solutionहाइड्रोजनपरमाणुकेप्रथमबोरकक्षककीत्रिज्याrहै,तबLi^(2+) के प्रथम कक्षक की त्रिज्या होगी :
View Solutionयदि दो वृतो की त्रिज्याएँ क्रमशः r1 व r2 है और वे एक - दूसरे को बाह्यतः स्पर्शः करते हो , तो -
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2
View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can
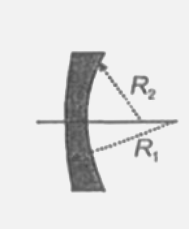
View SolutionIn a ΔABC, if 2r2r3r2−r1=r3−r1 then
r1(r2+r3)√r1r2+r2r3+r3r1=
View Solutionत्रिज्याओं r1 व r2(r1>r2) के दो गोलों को संयोजित किया जाता है। यदि परिणामी ठोस का गुरुत्व केंद्र r1 त्रिज्या वाले गोले के केंद्र से r1+r23 दूरी पर केंद्रों को मिलाने वाली रेखा पर स्थित है। r1:r2 है
View SolutionTwo circles with radii r1 and r2,r1>r2≥2 touch others externelly. If α is the angle between direct common tangents then sinα2=r1−r2r1+r2
View SolutionIn any triangle ABC,r1,r2+r2r3+r3r1=....
View SolutionIn any triangle ABc,r1r2+r2r3+r3r1=
View SolutionIf R1andR2 are the radii of curvature of the spherical surfaces of a thin lens and R1>R2, then this lens can

View Solution
