13r+8v=47
22v=63−17r
Based on the system of equations above, what is the sum of r and v?
The correct Answer is:113 OR 3.67
To solve the system of equations given by:
1. 13r+8v=47
2. 22v=63−17r
we will follow these steps:
Step 1: Rewrite the second equation in standard form
The second equation is not in standard form (where all variables are on one side and constants on the other). We can rearrange it:
22v+17r=63
2. 22v=63−17r
The second equation is not in standard form (where all variables are on one side and constants on the other). We can rearrange it:
Topper's Solved these Questions
Similar Questions
Knowledge Check
A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
An n-p-n transistor in a common - emitter mode is used as a simple voltage amplifier with a collector current of 4 mA. The positive terminal of a 8 V battery is connected to the collector through a load resistance RL and to the base through a resistance RB . The collector - emitter voltage VCE=4V , the base - emitter voltage VBE=0.6V and the current amplification factor β=100 . Calculate the values of RL and RB .
View SolutionProve that Cp−Cv=R.
View SolutionLet Vr denote the sum of the first r terms of an arithmetic progression (AP) whose first term is r and the common difference is (2r−1).LetT_r=V_(r+1)-V_r-2 and Q_r =T_(r+1)-T_r for r=1,2T_r is always (A) an odd number (B) an even number (C) a prime number (D) a composite num,ber
View SolutionIn the figure show,
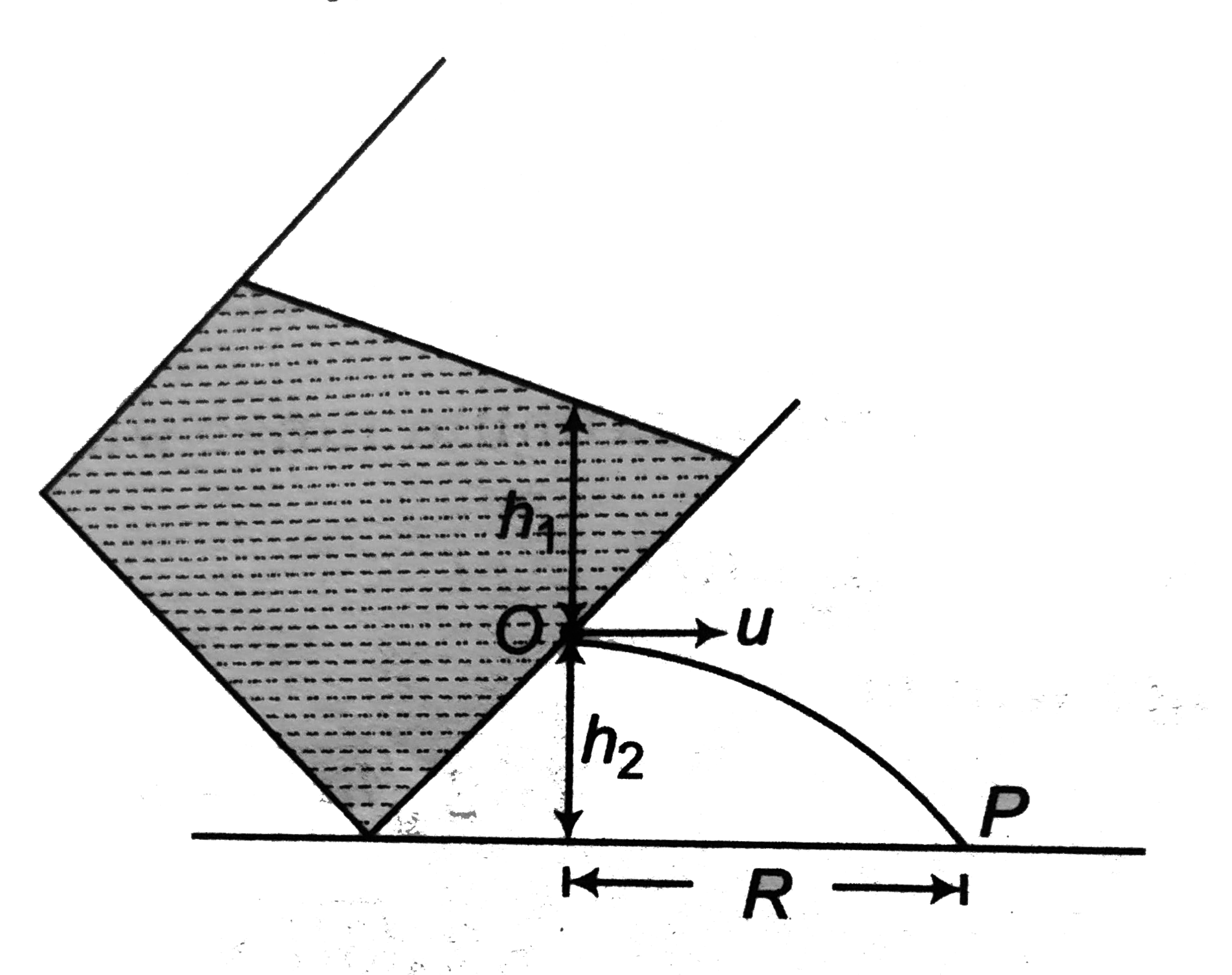
find v,top and R.
View SolutionFind the differential equations corresponding to v=Ar+B.
View SolutionLet V and I respresent, respectively, the readings of the voltmeter and ammetre shows in Fig. 6.34, and let RV and RV be their equivalent resistances. Because of the resistances of the meters, the resistnce R is not simply equal to V/I.
(a) When the circuit is connected as shows in Fig. 6.34 (a), shows that R=VI−RA
Explain why the true resistance R is always less than V/I.
(b) When the connections are as shows in Fig.6.34 (b)
Show that R=VI−(V/RV)
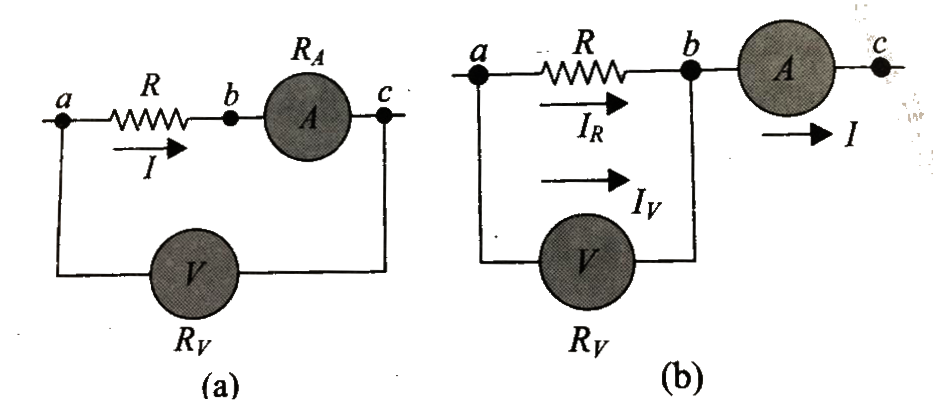
Explain why the true resistance R is always greater than V/I.
(c ) Show that the power delivered to the resistor in part
(i) is IV−I2RA and that in part (ii) is IV−(V2/RV)
View SolutionSolve the following system of equations: 15u+2v=17, 1u+1v=365
View Solution
