If d>aandL<a, which of the following cannot be true?
d+L=14
d−L=7
d−L=1
a−d=9
The correct Answer is:D
To solve the problem, we need to analyze the given inequalities and determine which of the options cannot be true based on the conditions d>a and L<a.
1. Understand the Given Conditions:
- We have two inequalities:
- d>a (which implies d−a>0)
- L<a (which implies L−a<0)
2. Rearranging the Inequalities:
- From d>a, we can rearrange it to a−d<0.
- From L<a, we can rearrange it to a−L>0.
3. Analyzing Each Option:
- We need to evaluate each option provided in the question to see if they can be true or not.
4. Option Analysis:
- Option 1: D+L=14
- We cannot determine if this is true or false based on the inequalities alone, so it might be true.
- Option 2: D−L=1
- Since d>a and L<a, it implies d>L. Therefore, D−L>0 which can be true.
- Option 3: D−L=7
- Similar to option 2, since d>L, D−L>0 which can also be true.
- Option 4: A−D=9
- Rearranging gives A=D+9. Since d>a, this means d cannot be A+9 (as d would have to be less than A), which contradicts d>a. Thus, this option cannot be true.
5. Conclusion:
- The option that cannot be true is Option 4: A−D=9.
- We have two inequalities:
- d>a (which implies d−a>0)
- L<a (which implies L−a<0)
- From d>a, we can rearrange it to a−d<0.
- From L<a, we can rearrange it to a−L>0.
- We need to evaluate each option provided in the question to see if they can be true or not.
- Option 1: D+L=14
- We cannot determine if this is true or false based on the inequalities alone, so it might be true.
- Option 2: D−L=1
- Since d>a and L<a, it implies d>L. Therefore, D−L>0 which can be true.
- Option 3: D−L=7
- Similar to option 2, since d>L, D−L>0 which can also be true.
- Option 4: A−D=9
- Rearranging gives A=D+9. Since d>a, this means d cannot be A+9 (as d would have to be less than A), which contradicts d>a. Thus, this option cannot be true.
- The option that cannot be true is Option 4: A−D=9.
Similar Questions
In Figure, ABCD is a parallelogram. O is any point on AC.PQ ||AB and LM||AD. Prove that ar(parallelogramDLOP)= ar (parallellogramBMOQ)
View SolutionIn a △ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( △LCM)=ar (△LBM)
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( LBC)= ar ( MBC)
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( LOB)=ar ( MOC).
View SolutionIn a △ ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar (△ LOB)=ar (△ MOC)
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( ABM)=ar ( ACL).
View SolutionDiagonals of a parallelogram ABCD intersect at O..AL and CM are perpendiculars to BD such that L and M lie on BD . IS AL=CM? why or why not?
View Solution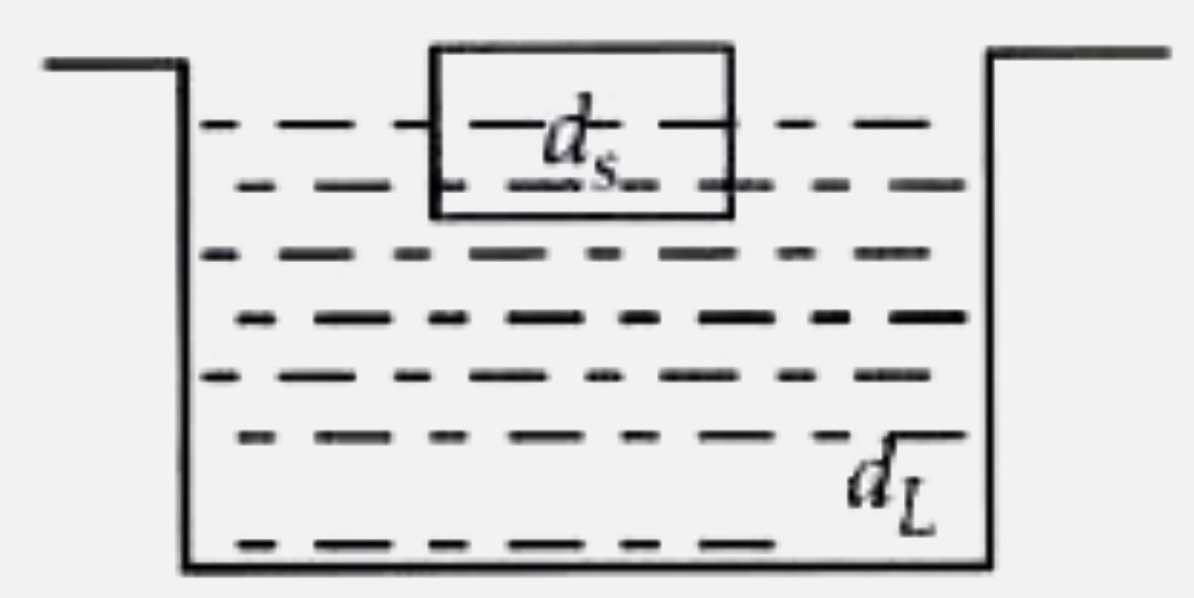
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the relation between dS and dL in the above case?
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionIn the given figure AB is the diameter of the circle, centred at O. If ∠COA=600,AB=2r,AC=d, and CD=l , then l is equal to (a) d√3 (b) d/√3 (c) 3d (d) √3 d /2
View Solution
