For a set of five true/false questions, no student has written all correct answers, and no two students have given the same sequence of answers. What is the maximum number of students in the classes, for this to be possible?
To solve the problem, we need to determine the maximum number of students who can answer a set of 5 true/false questions under the given conditions.
1. Determine the Total Possible Answers:
Each question can be answered in 2 ways (True or False). Since there are 5 questions, the total number of possible answer sequences is given by:
25=32
2. Account for the Condition of Correct Answers:
The problem states that no student has written all correct answers. This means that there is one specific sequence (where all answers are correct) that cannot be used.
3. Subtract the All-Correct Sequence:
Since there is only one sequence where all answers are correct (i.e., all True), we need to subtract this one sequence from the total number of possible sequences:
Maximum number of students=32−1=31
4. Conclusion:
Therefore, the maximum number of students in the class, such that no student has written all correct answers and no two students have given the same sequence of answers, is:
31
Each question can be answered in 2 ways (True or False). Since there are 5 questions, the total number of possible answer sequences is given by:
25=32
The problem states that no student has written all correct answers. This means that there is one specific sequence (where all answers are correct) that cannot be used.
Since there is only one sequence where all answers are correct (i.e., all True), we need to subtract this one sequence from the total number of possible sequences:
Maximum number of students=32−1=31
Therefore, the maximum number of students in the class, such that no student has written all correct answers and no two students have given the same sequence of answers, is:
31
Topper's Solved these Questions
Similar Questions
For a set of five true or false questions, no student hs written the all correct answer and no two students have given the same sequence of answers. What is the maximum number of students in the class for this to be possible?
View SolutionFollowing histogram depicts the range of heights of students in a class of 60 students. Study the same and answer the questions.
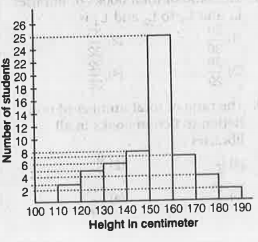
Which group contains maximum number of students ?
View Solution
Knowledge Check
For a set of four multiple choice questions with three options (multiple correct possible), no two students have given the same sequence of answers. What is the maximum number of students that sat for the test, for this to be possible, given that each student attempts all the questions. No student gives all the correct answers?
A4095B2400C1295D2500Following histogram depicts the range of heights of students in a class of 60 students. Study the same and answer the questions.
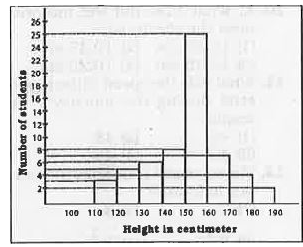
Group which contains maximum number of students isA130 - 140B150 - 160C140 - 150D160 - 170There are 60 questions in a question paper. If no two students solve the same combination of questions but solve equal number of questions, then the maximum number of student who appeared in the examination, is
A60C29B60C30C60C50Dnone of these
In a test, 6 questions are of the form ‘state, true or false’. No student has got all answers correct. Also, the answer of every student is different. Then the number of students appeared for the test
View SolutionStudy the following histogram of marks in mathematics (out of 50) of students in a class and answer the following questions.
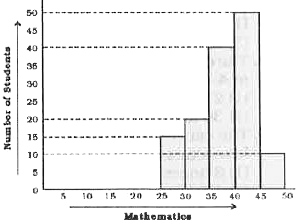
The total number of students in the class is :
View SolutionFollowing histogram depicts the range of heights of students in a class of 60 students. Study the same and answer the questions.
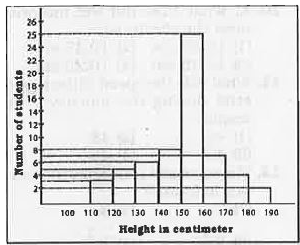
The number of students having their heights between 130 to 150 cms is
View SolutionFollowing histogram depicts the range of heights of students in a class of 60 students. Study the same and answer the questions.
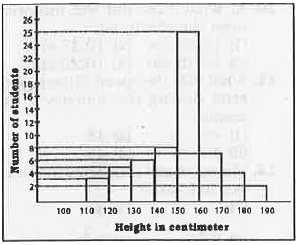
The number of students having height more than 150 cms is
View SolutionThese questions consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided to the statements are sufficient to answer the question. Read both the statements and select the appropriate answer
How many students are there in the class?
I. There are more than 20 but less than 27 students in the class.
II. There are more than 24 but than 31 students in the class. The number of students in the class can be divided into groups such that each group contains 5 students.
View Solution
