Two wires of the same length and material but different radii r1 and r2 are suspended from a rigid support both carry the same load at the lower end. The ratio of the stress devedoped in the second wire to that developed in the first wire is
r1r2
r21r22
(r1r2)5/2
(r1r2)1/2
The correct Answer is:B
To solve the problem, we need to find the ratio of the stress developed in the second wire to that developed in the first wire. Let's go through the steps systematically.
1. Understanding Stress:
Stress (σ) is defined as the force (F) applied per unit area (A). Mathematically, it can be expressed as:
σ=FA
2. Identify the Forces:
Both wires are carrying the same load (W). Therefore, the force acting on both wires is the same:
F1=F2=W
3. Cross-Sectional Area:
The cross-sectional area (A) of a wire with radius r is given by:
A=πr2
Thus, for wire 1 (with radius r1):
A1=πr21
For wire 2 (with radius r2):
A2=πr22
4. Calculate Stress for Each Wire:
Using the formula for stress, we can write the stress for wire 1 (σ₁) and wire 2 (σ₂):
σ1=WA1=Wπr21
σ2=WA2=Wπr22
5. Finding the Ratio of Stresses:
To find the ratio of the stress in wire 2 to the stress in wire 1, we can set up the following equation:
σ2σ1=Wπr22Wπr21=r21r22
6. Final Result:
Therefore, the ratio of the stress developed in the second wire to that developed in the first wire is:
σ2σ1=r21r22
Conclusion:
The ratio of the stress developed in the second wire to that developed in the first wire is r21r22.
---
Stress (σ) is defined as the force (F) applied per unit area (A). Mathematically, it can be expressed as:
σ=FA
Both wires are carrying the same load (W). Therefore, the force acting on both wires is the same:
F1=F2=W
The cross-sectional area (A) of a wire with radius r is given by:
A=πr2
Thus, for wire 1 (with radius r1):
A1=πr21
For wire 2 (with radius r2):
A2=πr22
Using the formula for stress, we can write the stress for wire 1 (σ₁) and wire 2 (σ₂):
σ1=WA1=Wπr21
σ2=WA2=Wπr22
To find the ratio of the stress in wire 2 to the stress in wire 1, we can set up the following equation:
σ2σ1=Wπr22Wπr21=r21r22
Therefore, the ratio of the stress developed in the second wire to that developed in the first wire is:
σ2σ1=r21r22
The ratio of the stress developed in the second wire to that developed in the first wire is r21r22.
Topper's Solved these Questions
- ELASTICITYBook:MOTIONChapter:ELASTICITYExercise:EXERCISE -2
Explore 25 Videos
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -4 (Level -II)
Explore 25 Videos
- ELASTICITY AND THERMAL EXPANSIONBook:MOTIONChapter:ELASTICITY AND THERMAL EXPANSIONExercise:Exercise - 4 (Level-II)
Explore 11 Videos
Similar Questions
Two wires of same length and material but of different radii are suspended from a rigid support. Both carry the same load. Will the stress, strain and extension in them be same or different ?
View SolutionTwo wires of same material and same length have radii r1andr2 respectively. Compare their resistances.
View Solution
Knowledge Check
Two wires A and B of same length and of the same material have the respective radii r1 and r2. Their one end is fixed with a rigid support, and at other end equal twisting couple is applied. Then the ratio of the angle of twist at the end of A and the angle of twist at the end of B will be
Ar21r22Br22r22Cr42r41Dr41r42The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
A1:1B1:2C2:1D4:1A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
AThe loss in gravitational potential energy of mass M is Mgl.BThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is loss of mechanical energy of system is 12Mgl
A composite wire of length 2L is made by joining two different wires A and B having the same length, made of the same material but of different radii r and 2r respectively . The composite wire is vibrating at such a frequency, that the junction of the two wires form a node. If the number of antinodes in the wire A is p and that in the wire B is q, then the ratio p:q is
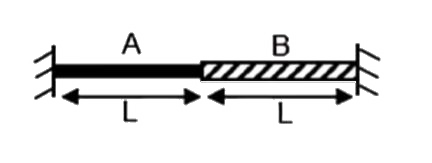
View SolutionTwo wires of the same length and same material but radii in the ratio of 1:2 are stretched by unequal forces to produce equal elongation. The ratio of the two forces is
View SolutionAn aluminum wire and a steel wire of the same length and cross-section are joined end to end. The compoiste wire is hung from a rigid support and a load is suspended from the free end. If the length of the composite wire is 2.7mm then the increases in the length of wire is (in mm)
(YAl=2×1011Nm2,YSteel=7×1011Nm−2)
View SolutionTwo wires of the same material have masses in the ratio of their extenisons under the same load if their lenghts are in the ratio 9:10 is
View SolutionTwo wires of the same material but of different diameters carry the same current i. If the ratio of their diameters is 2:1 , then the corresponding ratio of their mean drift velocities will be
View Solution

