Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.

∵ The elongation is steel wire Δls=Mglsπr2Ys
=(4+6)×9.8×1.53.14×(0.125×10−2×2×1011)=1.50×10−4m
Topper's Solved these Questions
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - QUESTION FOR PRACTICE
3 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -1
27 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -4 (Level -II)
25 Videos
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 4 (Level-II)
11 Videos
Similar Questions
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
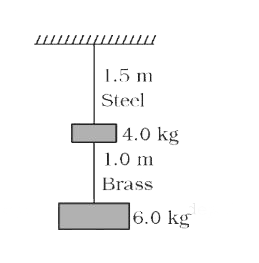
View SolutionTwo wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?

View Solution
Knowledge Check
Two wires of equal cross-section but one made of steel and the other of copper are joined end to end. When the cobination is kept under tension, the elongations in the two wires are found to be equal elongations in the two wire are found to be equal. What is the ratio of the lengths of the two wires?
(Given, Young's modulus of steel =2×1011Nm−2 and young's modulus of copper =1.1×1011Nm−2)A2:11B11:2C20:11D11:20The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
A1:1B1:2C2:1D4:1The Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
A1:1B1:2C2:1D4:2
Compute the elongation of the steel wire and brass wire in the given
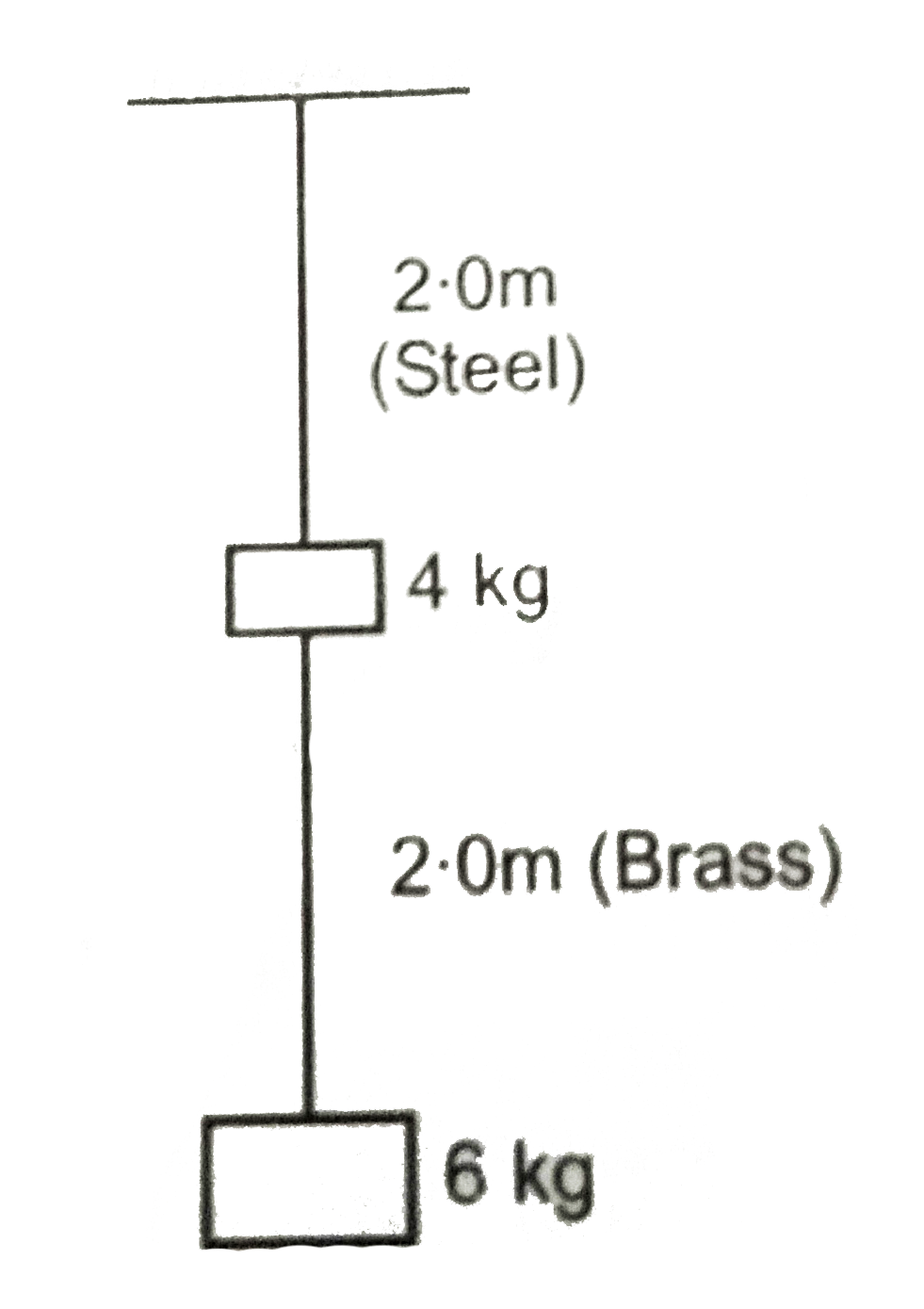
Given unloaded length of steel wire = 2.0 m, unloaded length of brass wire = 1.0m. Area of cross-section of each wire =0.049cm2.
Ysteel=2×1011Pa
and YBrass=0.90×1011Pa,g=9.8ms−2
View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View SolutionTwo wires of equal cross section but one made of steel and the other of copper, are joined end to end. When the combination is kept under tension, the elongations in the two wires are found to be equal. Find the ratio of the lengths of the two wires. Young modulus of steel =2.0×1011Nm−2 and that of copper =1.1×101Nm−2
View SolutionA weight of 100N is suspended by two wires made by steel and copper as shown in figure length of steel wire is 1m and copper wire is √3m. Find ratio of change in length of copper wire (Δlc) to change in length of steel wire (Δls). given Young's modulus YSteel=2×1011N/m2,YCopper=1×1011N/m2
_PHY_E01_017_Q01.png)
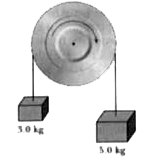
View SolutionThe figure shows two creates that are connected by a steel wire that passes over a pulley. The unstretched length of the wire is 1.5 m, and its cross - sectional area is 1.3×10−5m2. The pulley is frictionless and massless. When the crates are accelerating, determine the change in length of the wire. Ignore the mass of the wire.
View Solution
