Holes are drilled along the diameter of a disc. For a minimum time period, the disc should be suspend from the centre of gravity at a distance of :
R
R2
R√2
Zero
The correct Answer is:C
Step by step video, text & image solution for Holes are drilled along the diameter of a disc. For a minimum time period, the disc should be suspend from the centre of gravity at a distance of : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - A Previous Year Problems | NEET
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum
6 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]
11 Videos
Similar Questions
A uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionThree identical discs A, B, and C (figure) rest on a smooth horizontal plane. The disc A is set in motion with vector v after which it experiences an elastic collision simultaneously with the discs B and C. The distance between the centres of the latter discs prior of the collision is η times greater than the diameter of each disc.
Find the velocity of the disc A after the collision. At what value of η will the disc A recoil after the collision, stop, move on?

View Solution
Knowledge Check
A number of holes are drilled along a diameter of a disc of radius R. To get minimum time period of oscillations the disc should be suspended from a horizontal axis passing through a hole whose distance from the centre should be
AR2BR√2CR2√2DzeroIf a hole is drilled along the diameter of the earth and you leave a coin in the hole, then
Ait falls off and leaves the earthBit falls off and finally stops at the centre of the earthCit falls off but does not leave the earthDit falls and comes back to youA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A335cmB135cmC310cmDNone of these
Show that the time period of a compound pendulam is minimum when it is suspended from a point at a distance equal to its radius of gyration.
View SolutionA uniform disc of radius r is to be suspended through a small hole made in te disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA disc of mass 'm' and radius R is free to rotate in horizontal plane about a vetical smooth fixed axis passing through is centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in fig. The disc is given initial angular velocity ω0 and released. The angular speed of the disc when the balls reach the end of the disc is -
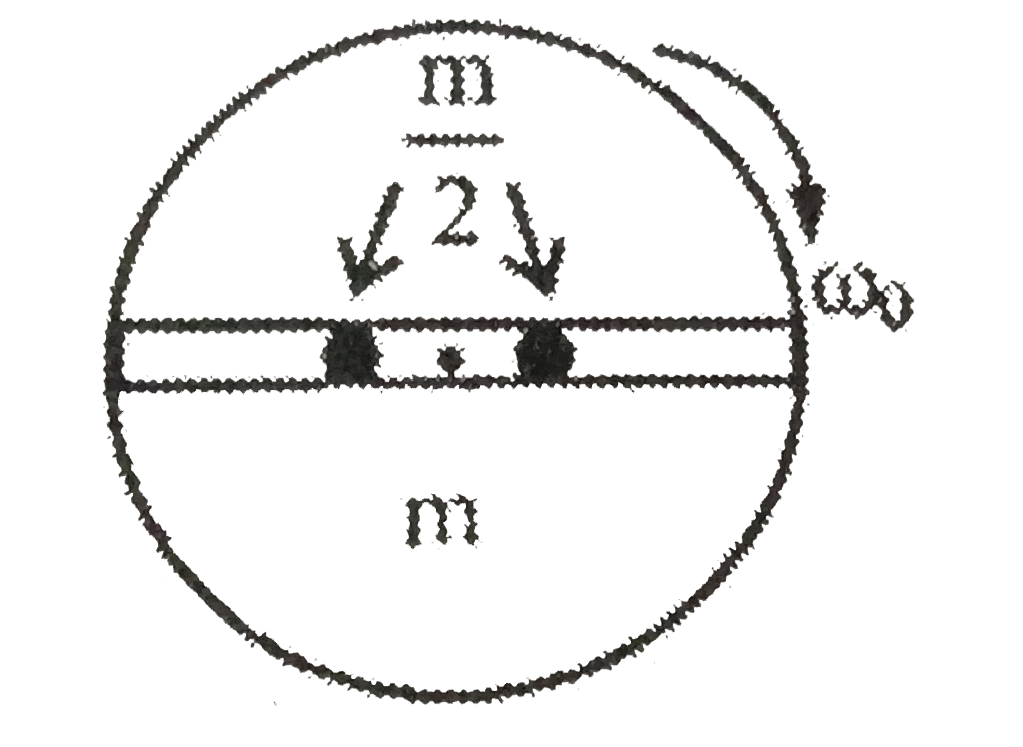
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View Solution
