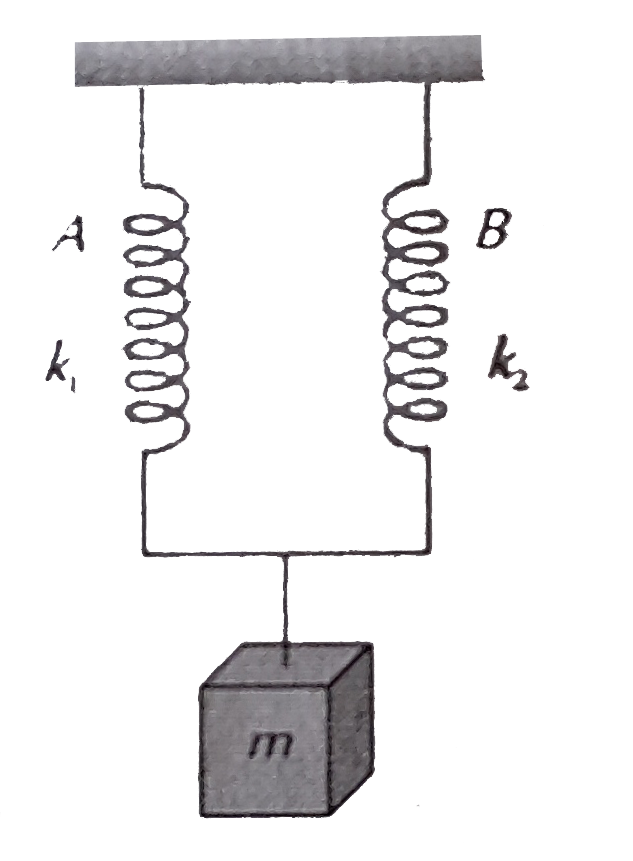
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are $k_{1} and k_{2} .$ The time period of the suspended mass will be

A

$T = 2 π \sqrt{(\frac{m}{K_{1} - K_{2}})}$

B

$T = 2 π \sqrt{(\frac{m}{K_{1} - K_{2}})}$

C

$T = 2 π \sqrt{(\frac{m (K_{1} + K_{2})}{K_{1} K_{2}})}$

D

$T = 2 π \sqrt{(\frac{m K_{1} K_{2}}{K_{1} + K_{2}})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

|

Answer

Step by step video, text & image solution for A mass m is suspended from the two coupled springs connected in series. The force constant for springs are k_(1) "and" k_(2). The time period of the suspended mass will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A mass m is suspended from the two coupled springs connected in series. The force constant for spring are $k_{1}$ and $k_{2}$ . The time period of the suspended mass will be:
A $T = 2 π \sqrt{\frac{m}{k_{1} - k_{2}}}$
B $T = 2 π \sqrt{\frac{m k_{1} k_{2}}{k_{1} + k_{2}}}$
C $T = 2 π \sqrt{\frac{m}{k_{1} + k_{2}}}$
D $T = 2 π \sqrt{\frac{m (k_{1} + k_{2})}{k_{1} k_{2}}}$
Question 2 - Select One
A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are $k_{1} and k_{2}$ respectively. When set into vertical vibrations, the period will be

A $2 π \sqrt{(\frac{m}{k_{1} k_{2}})}$
B $2 π \sqrt{m (\frac{k_{1}}{k_{2}})}$
C $2 π \sqrt{(\frac{m}{k_{1} - k_{2}})}$
D $2 π \sqrt{(\frac{m}{k_{1} + k_{2}})}$
Question 3 - Select One
A mass $m$ is suspended separately by two different springs of spring constant $k_{1}$ and $k_{2}$ given the time period $t_{1}$ and $t_{2}$ respectively. If the same mass $m$ is shown in the figure then time period $t$ is given by the relation

A $t = t_{1} + t_{2}$
B $t = \frac{t_{1} t_{2}}{t_{1} + t_{2}}$
C $t^{2} = t_{1}^{2} + t_{2}^{2}$
D $t^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$

MOTION-SIMPLE HARMONIC MOTION-EXERCISE (Questions For Practice)

Home
Ask Doubt
Profile