When the current flowing in a galvanometer is (1/n) of the total current, the resistance of the shunt will be
G/n
(n−1)G
G/(n−1)
G/(n2−1)
The correct Answer is:C
To find the resistance of the shunt when the current flowing in the galvanometer is 1n of the total current, we can follow these steps:
1. Understand the Current Relationship:
- Let I be the total current flowing through the circuit.
- The current through the galvanometer Ig is given as Ig=In.
- Therefore, the current through the shunt Is can be expressed as:
Is=I−Ig=I−In=I(1−1n)=I(n−1n)
2. Apply Ohm's Law:
- The potential difference across the galvanometer Vg can be expressed using Ohm's law:
Vg=Ig⋅G
- Where G is the resistance of the galvanometer.
3. Potential Difference Across the Shunt:
- The potential difference across the shunt Vs is the same as that across the galvanometer because they are in parallel:
Vs=Is⋅S
- Where S is the resistance of the shunt.
4. Equate the Potentials:
- Since Vg=Vs, we can write:
Ig⋅G=Is⋅S
5. Substitute the Values:
- Substitute Ig and Is into the equation:
(In)⋅G=(I⋅n−1n)⋅S
6. Simplify the Equation:
- Cancel I from both sides (assuming I≠0):
Gn=(n−1)n⋅S
7. Solve for the Shunt Resistance S:
- Rearranging gives:
S=Gn−1
Final Result:
Thus, the resistance of the shunt is:
S=Gn−1
- Let I be the total current flowing through the circuit.
- The current through the galvanometer Ig is given as Ig=In.
- Therefore, the current through the shunt Is can be expressed as:
Is=I−Ig=I−In=I(1−1n)=I(n−1n)
- The potential difference across the galvanometer Vg can be expressed using Ohm's law:
Vg=Ig⋅G
- Where G is the resistance of the galvanometer.
- The potential difference across the shunt Vs is the same as that across the galvanometer because they are in parallel:
Vs=Is⋅S
- Where S is the resistance of the shunt.
- Since Vg=Vs, we can write:
Ig⋅G=Is⋅S
- Substitute Ig and Is into the equation:
(In)⋅G=(I⋅n−1n)⋅S
- Cancel I from both sides (assuming I≠0):
Gn=(n−1)n⋅S
- Rearranging gives:
S=Gn−1
Thus, the resistance of the shunt is:
S=Gn−1
Topper's Solved these Questions
- Electrical Instrument Book:MOTIONChapter:Electrical Instrument Exercise:EXERCISE -2
Explore 21 Videos
- Electrical Instrument Book:MOTIONChapter:Electrical Instrument Exercise:EXERCISE -3
Explore 16 Videos
- Electrical Instrument Book:MOTIONChapter:Electrical Instrument Exercise:EXERCISE -3
Explore 16 Videos
- ELASTICITY AND THERMAL EXPANSIONBook:MOTIONChapter:ELASTICITY AND THERMAL EXPANSIONExercise:Exercise - 4 (Level-II)
Explore 11 Videos
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:EXERCISE-4| Section B (Prevous Years Problems )
Explore 29 Videos
Similar Questions
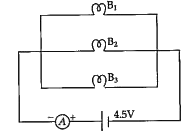
Total current flowing from the battery is 1A. Find the total resistance of the circuit:
View SolutionA galvanometer of resistance 3663Ω gives full scale deflection for a certain current ig. Calculate the resistance of the shunt which when joined to the galvanometer coil will result in 1/34 of the total current passing through the galvanometer. also finid the total resistnace of the galvanometer and the shunt.
View Solution
Knowledge Check
If only 1% of the total current is to be passed through a galvanometer of resistance G, then resistance of the shunt will be
AG25ΩBG25ΩCG49ΩDG99ΩIf only 2% of the main current is to be passed through a galvanometer of resistance G, then the resistance of the shunt will be
AG/50BG/49C50GD49GIf only 2% of the main current is to be passed through a galvanometer of resistance G , then the resistance of shunt will be
AG50BG49C50GD49G
Draw a schematic diagram of circuit consisting of a battery of 3 cells of 2V each, combination of three resistors 10ohm, 20ohm and 30ohm connected in parallel, a plug key and an ammeter,all connected in series. Use this circuit to find the following
(i) Current through each resistor.
(ii) Total current in circuit
(iii)Total Effective resistance of circuit
View SolutionSelect and write the corrcet answer :
When shunted , the current sensitivity of a galvanometer reduces by a factor of 100. The resistance of the shunt is
View SolutionIn an ammeter 5% of the main current is passing through the galvanometer. If the resistance of galvanometer is G, then the resistance of shunt S will be
View SolutionIn an ammeter 5% of the total current is passing through the galvanometer of resistance G. The resistance of shunt (S) required will be
View SolutionA galvanometer of coil resistance 100Ω is connected to a shunt of resistance 10Ω . The current through the galvanometer is i1 , the current through the shunt is i2 and the total current into the combination is i3 , then the ratio i1:i2:i3 is
View Solution

