Two particles move on a circular path (one just inside and the other just outside) with the angular velocities $ω$ and $5 ω$ starting from the same point. Then

they cross each other at regular intervals of time
$\frac{24 π}{4 ω}$ when their angular velocities are oppositely directed

they cross each other at points on the path subtending an angle of $60^{\circ}$ at the centre if their angular velocities are oppositely directed

they cross at intervals of time $\frac{π}{3 ω}$ if their angular velocities are oppositely directed

they cross each other at points on the path subtending $90^{\circ}$ at the centre if their angular velocities are in the same sense

Video Solution

Text Solution

Verified by Experts

If the angular velocities are oppositely directed, they meet at intervals of
time t = $\frac{2 π}{ω_{r e l}} = \frac{2 π}{6 ω} = \frac{π}{3 ω}$
Angle subtended at the centre by the crossing pint
$θ = ω t = \frac{π}{3} = 60^{\circ}$
When their angluar velocities are in the same direction,
t' = $\frac{2 π}{ω_{r e l}} = \frac{2 π}{4 ω} = \frac{π}{2 ω} and θ' = \frac{π}{2 ω} \times ω = \frac{π}{2}$

Updated on:21/07/2023

Class 12 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One or More
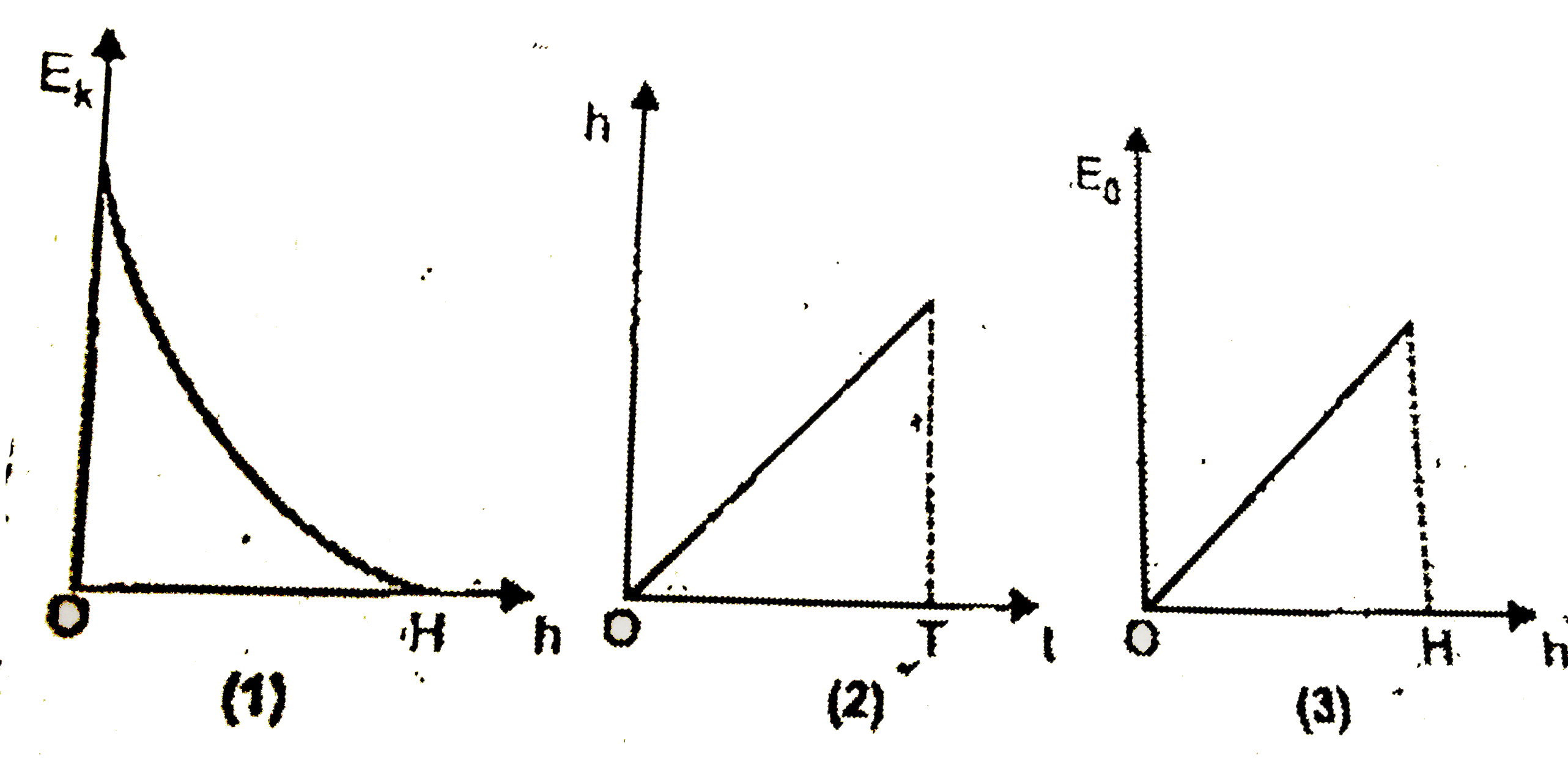
A ball is projected vertically upwards. Air resistance and variation in g may be neglected. The ball rises to its maximum height H in a time T, the height being h after a time t :
(1) The graph of kinetic energy $E_{k}$ of the ball against height h is shown in figure 1
(2) The graph of height h against time t is shown in figure 2
(3) The graph of gravitational energy $E_{k}$ of the ball against height h is shown in figure 3
(1)
Two particles move on a circular path ( one just inside and the other just outside) with angular velocities ro and $5 ω$ starting from the same point. Then :
Athey cross each other at regular intervals of time $\frac{2 π}{4 ω}$ when their angular velocities are oppositely directed
Bthey cross each other at points on the path subtending an angle of $60^{\circ}$ at the centre if their angular velocities are oppositely directed
Cthey cross at intervals of time $\frac{π}{3 ω}$ if their angular velocities are oppositely directed
Dthey cross each other .at points on the path subtending $90^{\circ}$ at the centre if their angular velocities are in the same sense
Question 2 - Select One
A particle moves in a circular path of radius 0.5 m with a linear speed of 2 $m s^{- 1}$ ,its angular speed is
A $2 r a d s^{- 1}$
B $3 r a d s^{- 1}$
C $4 r a d s^{- 1}$
DNone of these
Question 3 - Select One
A particle moving along a circule path of radius 'r' with uniform angular velocity $ω$ . Its angular acceleration is
A $r ω^{2}$
B $r / ω$
Czero
D $ω / r$

MOTION-CIRCULAR MOTION-EXERCISE - 4

Home
Ask Doubt
Profile

Two particles move on a circular path (one just inside and the other just outside) with the angular velocities ω and 5ω starting from the same point. Then

If the angular velocities are oppositely directed, they meet at intervals of time t = 2πωrel=2π6ω=π3ω Angle subtended at the centre by the crossing pint θ=ωt=π3=60∘ When their angluar velocities are in the same direction, t' = 2πωrel=2π4ω=π2ωandθ'=π2ω×ω=π2

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle moves in a circular path of radius 0.5 m with a linear speed of 2 ms−1 ,its angular speed is

A particle moving along a circule path of radius 'r' with uniform angular velocity ω. Its angular acceleration is

MOTION-CIRCULAR MOTION-EXERCISE - 4

Two particles move on a circular path (one just inside and the other just outside) with the angular velocities $ω$ and $5 ω$ starting from the same point. Then

A particle moves in a circular path of radius 0.5 m with a linear speed of 2 $m s^{- 1}$ ,its angular speed is

A particle moving along a circule path of radius 'r' with uniform angular velocity $ω$ . Its angular acceleration is