Given that P=Q=R. If →P+→Q=→R then the angle between →P&→R is θ1. If →P+→Q+→R=→0 then the angle between →P&→R is θ2. What is the relation between θ1andθ2 ?
A
θ1=θ2
B
θ1=θ22
C
θ1=2θ2
D
None of the above
Video Solution
Text Solution
The correct Answer is:B
Since P=Q=R
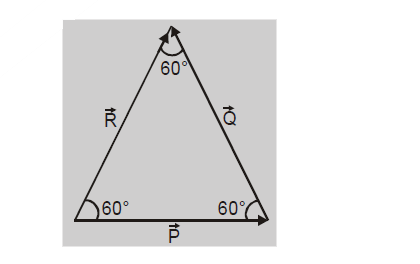
Therefore triangle formed by vectors →P,→Qand→R will be equilateral triangle.
Now if →P+→Q=→R, then →P&→Q will be in same order and →R will be in their reverse order.
From the diagram, angle between →P&→R=θ=60∘
But if →P+→Q+→R=→0 then →P,→Q&→R will be in same order
From the diagram, angle between
→P&→R=θ2=180∘−60∘=120∘
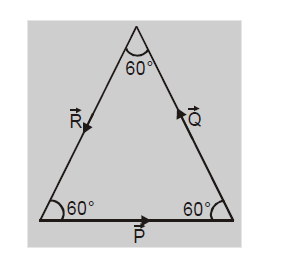
θ1θ2=60∘120∘=12⇒θ1=θ22
|
Topper's Solved these Questions
- VECTOR Book:MOTIONChapter:VECTOR Exercise:Exercise - 1
Explore 36 Videos
- VECTOR Book:MOTIONChapter:VECTOR Exercise:Exercise - 2
Explore 33 Videos
- UNITS AND DIMENSIONS, BASIC MATHEMATICS Book:MOTIONChapter:UNITS AND DIMENSIONS, BASIC MATHEMATICS Exercise:PRACTICE QUESTION
Explore 4 Videos
- VECTOR & CALCULUSBook:MOTIONChapter:VECTOR & CALCULUSExercise:EXERCISE -4 (LEVEL - II) PREVIOUS YEAR
Explore 15 Videos
Similar Questions
Knowledge Check
Given that P=Q=R. If →P+→Q=→R then the angle between →P and →R is θ1. If →P+→Q+→R=→0 then the angle between →P and →R is θ2. The relation between θ1 and θ2 is :-
Aθ1=θ2Bθ1=θ22Cθ1=2θ2DNone of theseIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
A0∘B90∘C180∘D45∘Given that P=Q=R. if →P+→Q=→R then the angle between →P&→R is θ1 then the angle between →P&→R is θ2. What is the relation between θ1 and θ2.
Aθ1=θ2Bθ1=θ12Cθ1=2θ2Dnone of the above
if ∣∣→P+→Q∣∣=∣∣→P∣∣+∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P∣∣−∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View SolutionWhat is the angle between →P and the resultant of (→P+→Q) and (→P−→Q)
View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1.If →P+→Q−→S=0 angle between →P and →S is θ2.The ratio of θ1 toθ2 is
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
View Solution