A perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
Let O be the centre of the sphere and OZ be the line opposite to the incident beam ( figure). Consider a radius about OZ to get amaking an angle θwith OZ. Rotate this radius about OZ to get a circle on the sphere. Change θ to θ+dθ and rotate the radius about OZ to get another circle on the sphere. The part of the sphere between these circles is a ring of area 2πr2sinθdθ. Consider a small part ΔA of this ring at P.Energyof light falling on this part in time Δt is
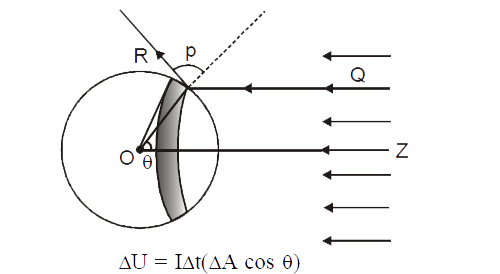
The momentum of this light falling on ΔA is ΔU/c along QP.The light is reflected by the sphere along PR. The change in momentum is
Δp=2ΔUccosθ=2cΔ(ΔAcos2θ) ( direction along →OP)
The force on ΔA due to the light falling on it, is
ΔpΔt=2cΔAcos2θ ( direction along →OP)
The resultant force on the ring as well as on the sphere is along ZO by symmetry . The component of the force on ΔA along ZO
ΔpΔtcosθ=2cIΔcos2θ ( along (→ZO)
The force acting on the ring is dF=2cI(2πr2sinθdθ)cos3θ
The force on the entire sphere is F=∫π/204πr2Iccos3θdθ
F=∫π/204πr2Iccos3θd(cosθ)
=−∫π/20−04πr2Ic[cos4θ4]π/20=πr2Ic
Note that integration is done only for the hemisphere that faces the incident beam.
Topper's Solved these Questions
- MODERN PHYSICS -1Book:MOTIONChapter:MODERN PHYSICS -1Exercise:EXERCISE-1
Explore 50 Videos
- MODERN PHYSICS -1Book:MOTIONChapter:MODERN PHYSICS -1Exercise:EXERCISE-2(LEVEL-I)
Explore 34 Videos
- MODERN PHYSICS - 2Book:MOTIONChapter:MODERN PHYSICS - 2Exercise:EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
Explore 28 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 3 Section-B
Explore 12 Videos
Similar Questions
A perfectly reflecting solid sphere of radius r is kept in the path of a parallel beam of light of large aperture. If the beam carries an intensity I, find the force exerted by the beam on the sphere.
View SolutionA sphere of radius 1.00 cm is placed in the path of a parallel beam of light of large aperture. The intensity of the light is 0.50 W cm−2. If the sphere completely absorbs the radiation falling on it, find the force exerted by the light beam on the sphere.
View Solution
Knowledge Check
A concave lens is placed in the path of a uniform parallel of beam of light falling on a screen as shown . Then
_E01_089_Q01.png) AIntensity of light will be the same every where on the screenBIntensity in region AB will be smaller that what it would be in the absence of the lensCIn the region AC and BD , the intensity will be smaller than what it would be in the absence of the lensDIn the region AC and BD, the intensity will be greater than what it would be in the absence of the lens
AIntensity of light will be the same every where on the screenBIntensity in region AB will be smaller that what it would be in the absence of the lensCIn the region AC and BD , the intensity will be smaller than what it would be in the absence of the lensDIn the region AC and BD, the intensity will be greater than what it would be in the absence of the lensA glass slab is placed in the path of a beam of convergent light. The point of convergence of light
Amoves towards the glass slabBmoves away from the glass slabCreamains at the same pointDundergoes a lateral shiftWhen a thin metal plate is placed in the path of one of the interfering beams of light
AFringe width increasesBFringes disappearCFringes become brighterDFringes becomes blurred
There is a parallel beam of light of larger aperture . Let I be the intensity of light . Perfectly reflecting sphere of radius r is kept in the path of this parallel beam . Find the force exerted by the light beam on sphere .
View SolutionA parallel beam of light falls on a solid tranparent sphere.
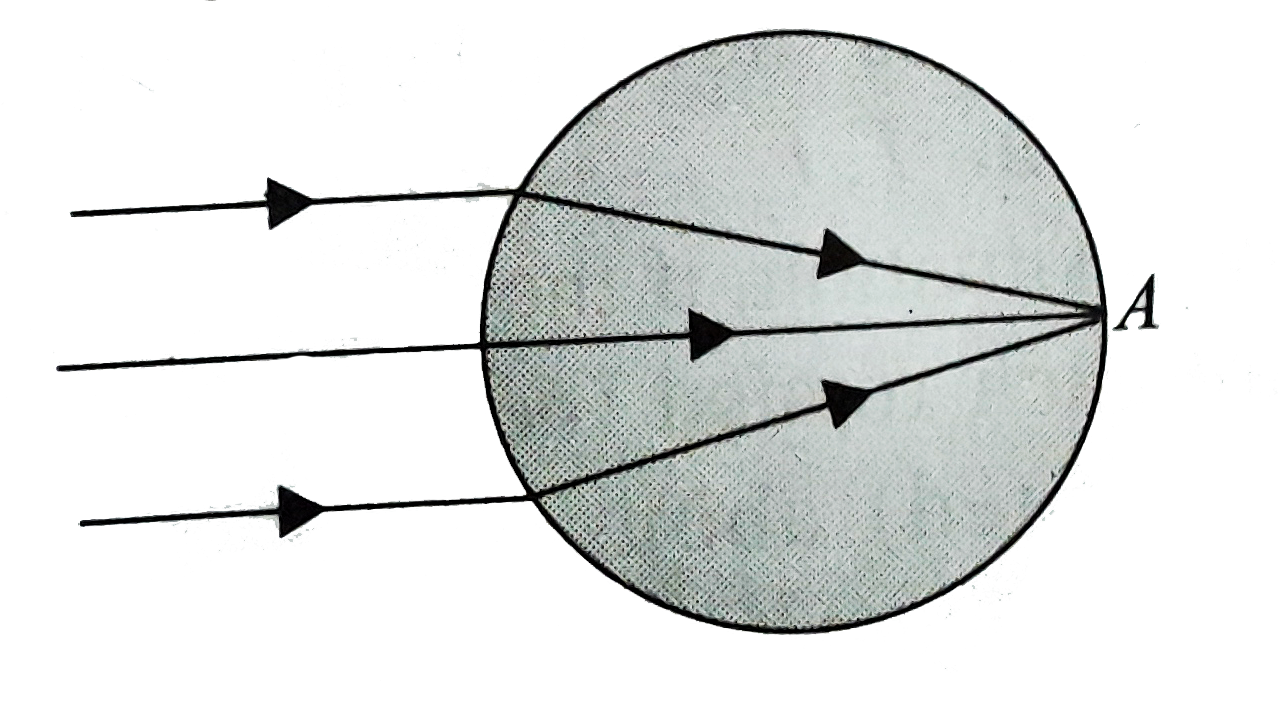
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA sphere of radius R is exposed to a parallel beam of radiation of intensity I as shown in figure. Choose the correct option (s) of the following.
View SolutionA parallel beam of the light is incident normally on a plane surface absorbing 40% of the light and reflecting the rest. If the incident beam carries 10 watt power, find the force exerted by it on the surface.
View SolutionA parallel beam of light falls on a solid tranparent sphere.
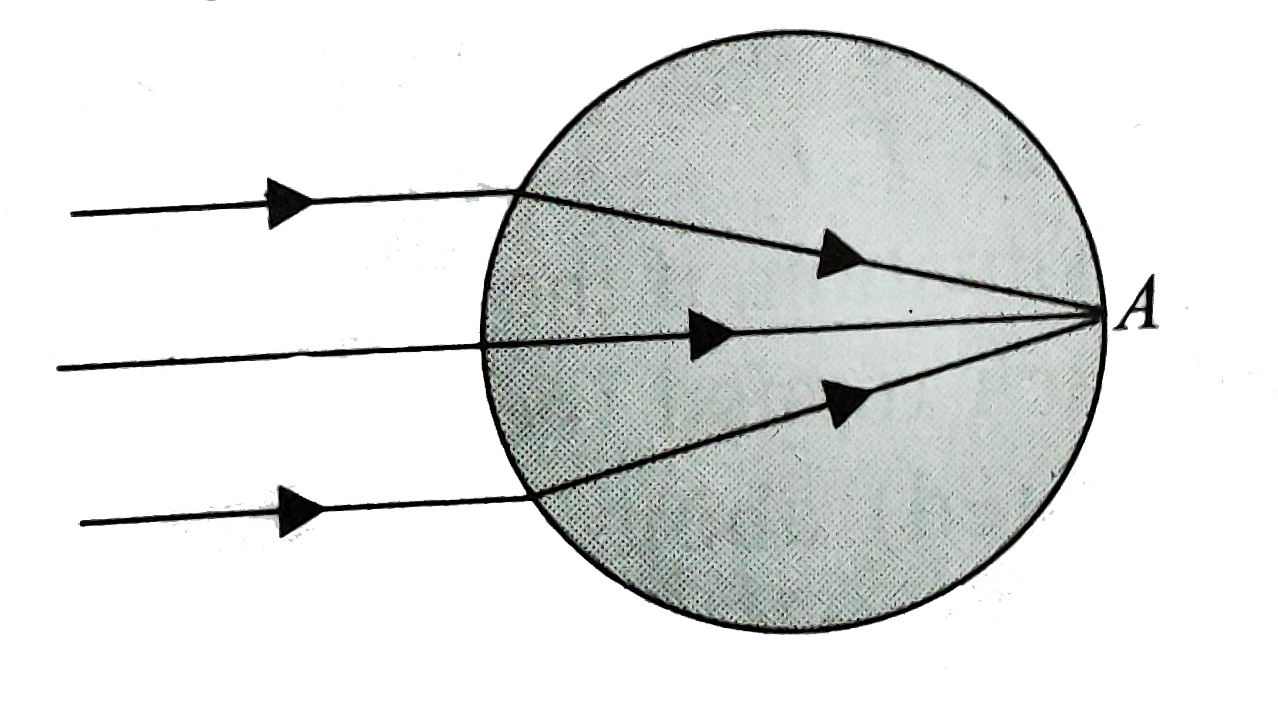
Q. Which is corret?
View Solution