Light is incident on the cathode of a photocell and the stopping voltages are measured from light of two difference wavelengths. From the data given below, determine the work function of the metal of the cathode in eV and the value of the universal constant hc/e.
Wavelength (Å) Stopping voltage (volt)
4000 1.3
4500 0.9
To solve the problem, we will follow these steps:
Step 1: Understand the Photoelectric Effect
The photoelectric effect states that when light of a certain frequency (or wavelength) hits a metal surface, it can eject electrons from that surface. The energy of the incoming photons is given by the equation:
E=hcλ
where:
- E is the energy of the photon,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the light.
The maximum kinetic energy (KEmax) of the emitted electrons can be expressed as:
KEmax=E−ϕ
where ϕ is the work function of the metal.
Step 2: Relate Stopping Voltage to Kinetic Energy
The stopping voltage (V0) is related to the maximum kinetic energy of the emitted electrons:
KEmax=eV0
where e is the charge of an electron. Therefore, we can express the stopping voltage as:
V0=KEmaxe=hceλ−ϕe
Step 3: Set Up the Equations for Two Wavelengths
From the data given:
1. For λ1=4000Å and V01=1.3V:
V01=hceλ1−ϕe
2. For λ2=4500Å and V02=0.9V:
V02=hceλ2−ϕe
Step 4: Subtract the Two Equations
Subtract the second equation from the first:
V01−V02=(hceλ1−ϕe)−(hceλ2−ϕe)
This simplifies to:
ΔV0=hce(1λ1−1λ2)
where ΔV0=V01−V02=1.3−0.9=0.4V.
Step 5: Solve for hce
Rearranging gives:
hce=ΔV0(1λ1−1λ2)
Substituting the values:
- λ1=4000Å=4000×10−10m
- λ2=4500Å=4500×10−10m
Calculating 1λ1−1λ2:
1λ1=14000×10−10=2.5×107m−1
1λ2=14500×10−10=2.222×107m−1
1λ1−1λ2=2.5×107−2.222×107=0.278×107m−1
Now substituting into the equation:
hce=0.40.278×107≈1.44×10−6V m
Step 6: Calculate Work Function ϕ
Using the first equation for V01:
1.3=hce⋅4000×10−10−ϕe
Rearranging gives:
ϕ=hc4000×10−10−1.3e
Substituting hce=1.44×10−6:
ϕ=1.44×10−64000×10−10−1.3
Calculating:
ϕ=3.6−1.3=2.3eV
Final Answers
- Work function ϕ=2.3eV
- Universal constant hce≈1.44×10−6V m
The photoelectric effect states that when light of a certain frequency (or wavelength) hits a metal surface, it can eject electrons from that surface. The energy of the incoming photons is given by the equation:
E=hcλ
where:
- E is the energy of the photon,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the light.
KEmax=E−ϕ
where ϕ is the work function of the metal.
The stopping voltage (V0) is related to the maximum kinetic energy of the emitted electrons:
KEmax=eV0
where e is the charge of an electron. Therefore, we can express the stopping voltage as:
V0=KEmaxe=hceλ−ϕe
From the data given:
1. For λ1=4000Å and V01=1.3V:
V01=hceλ1−ϕe
2. For λ2=4500Å and V02=0.9V:
V02=hceλ2−ϕe
Subtract the second equation from the first:
V01−V02=(hceλ1−ϕe)−(hceλ2−ϕe)
This simplifies to:
ΔV0=hce(1λ1−1λ2)
where ΔV0=V01−V02=1.3−0.9=0.4V.
Rearranging gives:
hce=ΔV0(1λ1−1λ2)
Substituting the values:
- λ1=4000Å=4000×10−10m
- λ2=4500Å=4500×10−10m
1λ1=14000×10−10=2.5×107m−1
1λ2=14500×10−10=2.222×107m−1
1λ1−1λ2=2.5×107−2.222×107=0.278×107m−1
hce=0.40.278×107≈1.44×10−6V m
Using the first equation for V01:
1.3=hce⋅4000×10−10−ϕe
Rearranging gives:
ϕ=hc4000×10−10−1.3e
Substituting hce=1.44×10−6:
ϕ=1.44×10−64000×10−10−1.3
Calculating:
ϕ=3.6−1.3=2.3eV
- Work function ϕ=2.3eV
- Universal constant hce≈1.44×10−6V m
Topper's Solved these Questions
- MODERN PHYSICS -1BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-1
50 Videos
- MODERN PHYSICS -1BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-2(LEVEL-I)
34 Videos
- MODERN PHYSICS - 2BOOK - MOTIONCHAPTER - MODERN PHYSICS - 2EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
Similar Questions
(a) If the wavelength of the light incident on a photoelectric cell be reduced from λ1 to λ2Å, then what will be the change in the cut-off potential?
(b) Light is incident on the cathode of a photocell and the stopping voltages are measured for light of two different wavelengths. From the data given below, determine the work function of the metal of the cathode in eV and the value of the universal constant hc/e.
WavelengthÅStopping voltage (volt)40001.345000.9
View SolutionElectrons are emitted from the cathode of a photocell of negligible work function, when photons of wavelength λ are incident on it. Derive the expression for the de Broglie wavelength of the electrons emitted in terms of the wavelength of the incident light
View Solution
Knowledge Check
If stopping potentials corresponding to wavelengths 4000A and 4500A are 1.3 V and 0.9 V, respectively, then the work function of the metal is
A0.3 eVB1.3 eVC2.3 eVD5 eVA metal is irradiated with light of wavelength 660 nm. Given that the work function of the metal is 1.0eV, the de Broglie wavelength of the ejected electron is close to-
A6.6×10−7mB8.9×10−11mC1.3×10−9mD6.6×10−13mLight from a hydrogen tube is incident on the cathode of a photoelectric cell the work function of the cathode surface is 4.2eV. In order to reduce the photo - current to zero the voltage of the anode relative to the cathode must be made
A−4.2VB−9.4VC−17.8VD+9.4V
Metal surface emits photoelectrons when light of wavelength 400 nm is incident on it. Calculate the work function of the metal if stopping potential is 0.5 V.
View SolutionThe cathode of a photocell is irradiated with light of wavelength 3000Å. The current through the cell is found to stop when the potential of the plate is 2.1 V just below the cathode. Calculate the work function of the cathode.
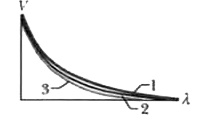
View SolutionIn the following figure gives the stopping voltage V versus the wavelength λ of light for three different materials. Rank the materials according to their work function, greatest first.
View SolutionThe radiation of wavelength 332 nm is incident on a metal of work function 1.70 eV. The value of the stopping potential will be
View SolutionLight from a hydrogen tube is incident on the cathode of a photoelectric cell the work function of the cathode surface is 4.2eV. In order to reduce the photo - current to zero the voltage of the anode relative to the cathode must be made
View Solution