Two thin conducting shells of radii R and 3R are as shown in the fig. External shell carries a charge +Q and inner shell neutral. The inner shell is earthed with the help of a switch S. Then

With the switch S open, the potential of the inner sphere is equal to that of the outer
When the switch S is closed, the potential of the inner sphere becomes zero
With the switch S closed, the charge attained by the inner sphere is –q/3
By closing the switch the capacitance of the system increases
The correct Answer is:A, B, C, D
Step by step video, text & image solution for Two thin conducting shells of radii R and 3R are as shown in the fig. External shell carries a charge +Q and inner shell neutral. The inner shell is earthed with the help of a switch S. Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -3 LEVEL 1
31 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -3 LEVEL II
17 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -2
36 Videos
- CALORIMETRY BOOK - MOTIONCHAPTER - CALORIMETRY EXERCISE - EXERCISE - 3 Section - B
4 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
Similar Questions
Two thin conducting shells of radii R and R ar shown in figure . The outer shell carries a charge +Q and the inner shell is neutral. The inner shell is earthed with the help of switch S . Find the charge attained by the inner shell.
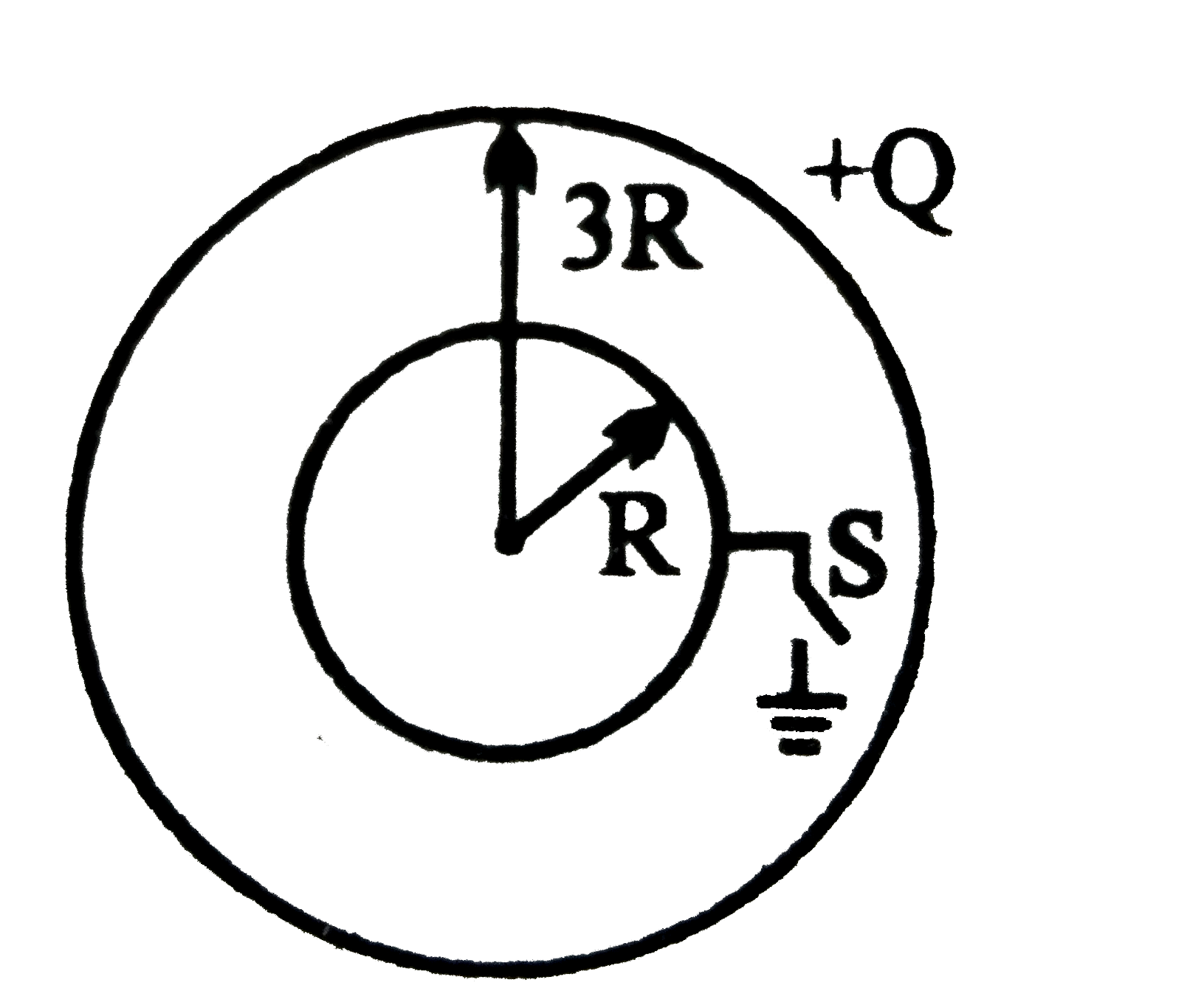 .
.
View Solution(Figure 3.158) shows two conducting thin concentric shells of radii r and 3r. The outer shell carries charge q and the inner shell is neutral . The amount of charge that flows from the inner shell to the earth after the key K is closed is equal to (1/n)th of the charge on the outer shell. What is the value of n ?
 .
.
View Solution
Knowledge Check
Figure shows two conducting thin concentric shells of radi r and 3r. The outer shell carries a charge q. Inner shell in neutral. Find the charge that wilL flow from inner shell to earth the switch S is closed.
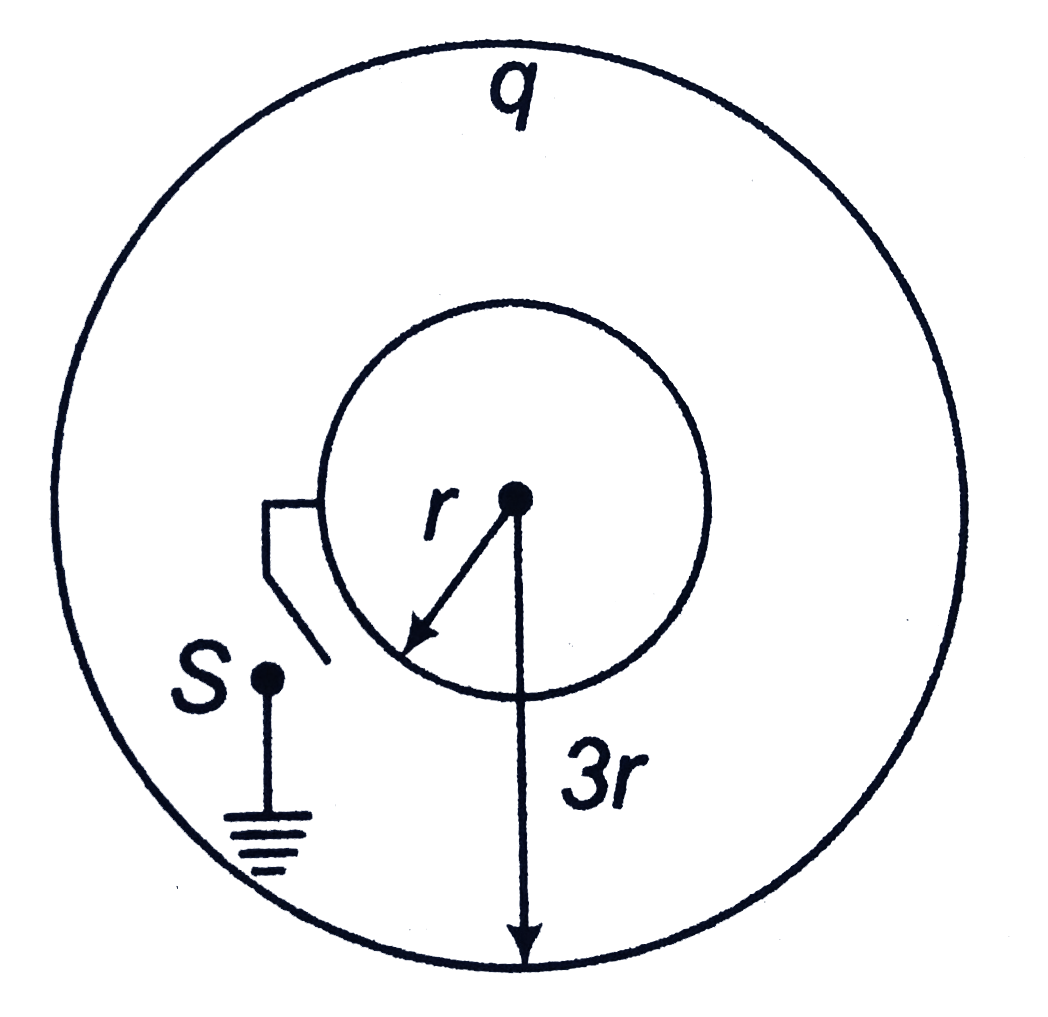 Aq3B−q3CqD−q
Aq3B−q3CqD−qIn the figure two concentric conducting shells of radius R & 2R are shown. The inner shell is charged with Q and the shell is unchanged. The amount of energy dissipated when the shells are connected by a conducting wire is:
 AKQ24RBkQ22RCkQ28RD3kQ24
AKQ24RBkQ22RCkQ28RD3kQ24There are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
A−QrRB−QRrC−2QRrD−Q)
Figure shows two conducting thin concentric shells of radii r and 3r . The outer shell carries charge q=6C .Inner shell is neutral.Find the charge (in C ) that will flow from inner shell to earth after the switch S is closed. qquad q=6c s
View SolutionFigure - shows two conducting thin concentric shells of radii r and 3r The outer shell carries charge q where as inner shell is uncharged. Find the charge that will flow from inner shell to earth after the switch S is closed.

[+q3 charge will flow inner shell to earth]
View SolutionTwo conducing concentric hollow spheres of radii a and 2a respectively are shown in the diagram. The inner shell has net charge Q on its surface. The outer shell is neutral. If the outer shell is connected to the earth the heat generated through the connecting wire is 2a
View SolutionThere are two concentric conducting spherical shells of radii 10 cm and 20 cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionTwo concentric thin conducting sphereical shells having radii R and 2R are as shown in the figure .A charge +Q is given to the shell A and −4Q is given to the shell B .If A and B are connected by a thin conducting wire then the amount of heat produced after the connection is

View Solution
