When a charge Q is given to a non conductuing plate & conducting plate. Find the ratio of electric field produced by them ?
To find the ratio of the electric field produced by a non-conducting plate and a conducting plate when a charge Q is given to both, we will follow these steps:
Step 1: Understand the charge distribution
- For a conducting plate, when a charge Q is given, the charge distributes itself uniformly on the surface of the conductor. This means that the electric field outside the conductor can be calculated using the surface charge density σ.
- For a non-conducting plate, the charge Q is distributed throughout the volume of the plate.
Step 2: Calculate the electric field for the conducting plate
- The electric field Ec due to an infinite conducting plane with surface charge density σ is given by:
Ec=σ2ϵ0
- The surface charge density σ can be expressed as:
σ=QA
where A is the area of the plate.
- Therefore, substituting σ into the electric field equation:
Ec=Q2Aϵ0
Step 3: Calculate the electric field for the non-conducting plate
- For a non-conducting plate with uniform surface charge density σ, the electric field En produced by one side of the plate is given by:
En=σ2ϵ0
- Since the non-conducting plate has charge distributed throughout its volume, the effective electric field on either side of the plate will be:
En=Q2Aϵ0
Step 4: Find the ratio of the electric fields
- Now, we can find the ratio of the electric fields produced by the non-conducting plate and the conducting plate:
Ratio=EnEc=Q2Aϵ0Q2Aϵ0=1
Conclusion
- The ratio of the electric field produced by the non-conducting plate to that produced by the conducting plate is:
Ratio=1
- For a conducting plate, when a charge Q is given, the charge distributes itself uniformly on the surface of the conductor. This means that the electric field outside the conductor can be calculated using the surface charge density σ.
- For a non-conducting plate, the charge Q is distributed throughout the volume of the plate.
- The electric field Ec due to an infinite conducting plane with surface charge density σ is given by:
Ec=σ2ϵ0
- The surface charge density σ can be expressed as:
σ=QA
where A is the area of the plate.
- Therefore, substituting σ into the electric field equation:
Ec=Q2Aϵ0
- For a non-conducting plate with uniform surface charge density σ, the electric field En produced by one side of the plate is given by:
En=σ2ϵ0
- Since the non-conducting plate has charge distributed throughout its volume, the effective electric field on either side of the plate will be:
En=Q2Aϵ0
- Now, we can find the ratio of the electric fields produced by the non-conducting plate and the conducting plate:
Ratio=EnEc=Q2Aϵ0Q2Aϵ0=1
- The ratio of the electric field produced by the non-conducting plate to that produced by the conducting plate is:
Ratio=1
Topper's Solved these Questions
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise 1 (Section A-Questions Based on electric flux for various configuration, Question on solid angle concept, Gauss law Based Questions)
Explore 16 Videos
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise 1 (Section B - Properties of conductors)
Explore 15 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
Explore 13 Videos
- ERRORS , THEORY Book:MOTIONChapter:ERRORS , THEORY Exercise:EXERCISE 4 (LEVEL -II)
Explore 10 Videos
Similar Questions
A positive point charge (+q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines originating from the point on to the surface of the plate.
Derive the expression for the electric field at the surface of a charged conductor.
View SolutionThe figure shows three infinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area +σ,+2σ and −σ. Find the ratio of the net electric field at that point a to that at point B.
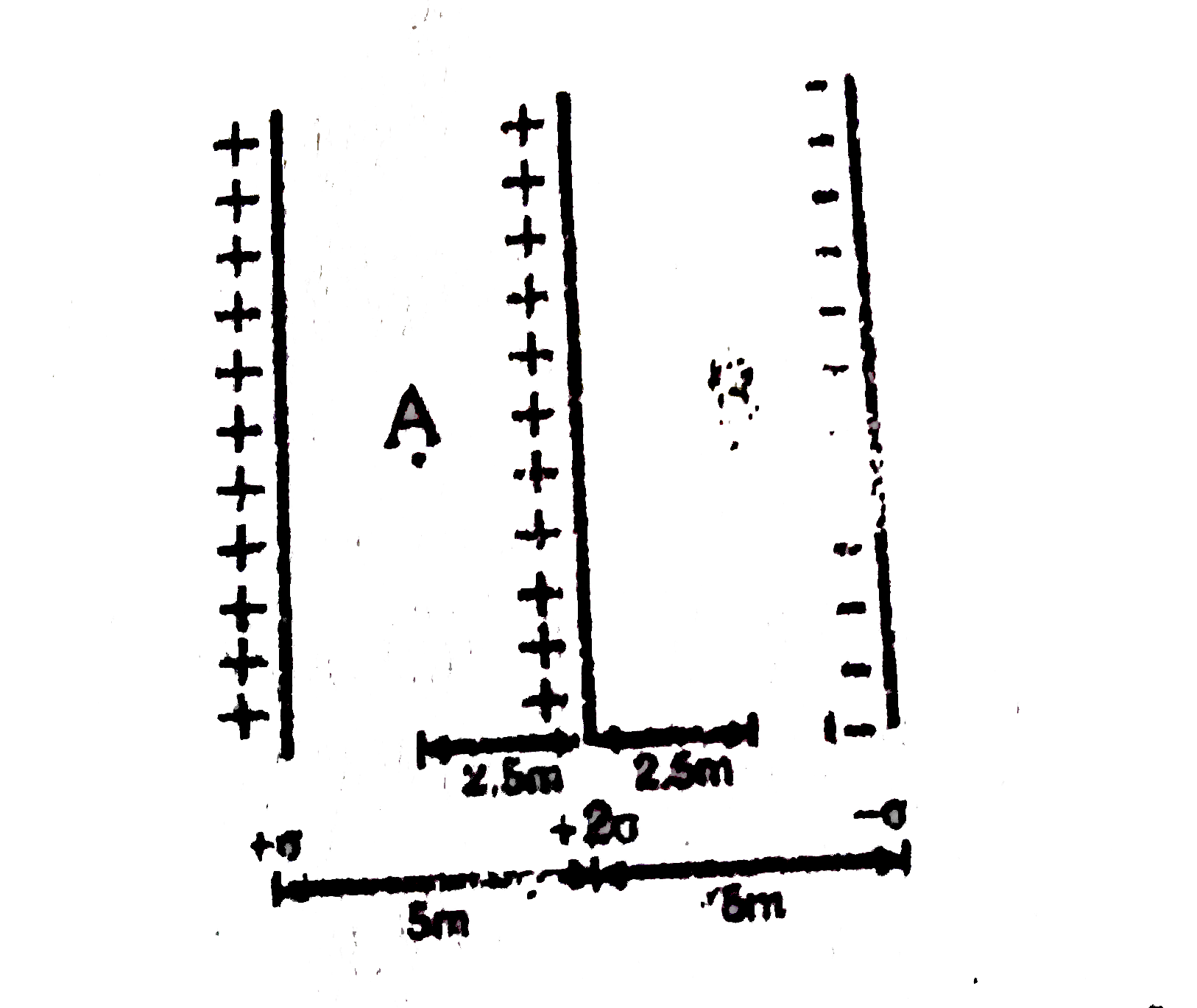
View Solution
Knowledge Check
Conduction electrons are almost uniformly distributed within a conducting plate. When placed in an electric field →E, the electric field within the plate
AIs zeroBDepends upon ECDepends upon →EDDepends upon the atomic number of the conducting elementThe plates of charged condenser are connected by a conducting wire. The quantity of heat produced in the wire is
AInversely proportional to the capacity of the condenserBInversely proportional to the square of the potential of the condenserCProportional to the length of wireDindependent of the resistance of the wire
The figure shows thrednfinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area +σ,+2σ and −σ . Find the ratio of the net electric field atthat point A to that at point B. The points A and Bare located midway between the plates :
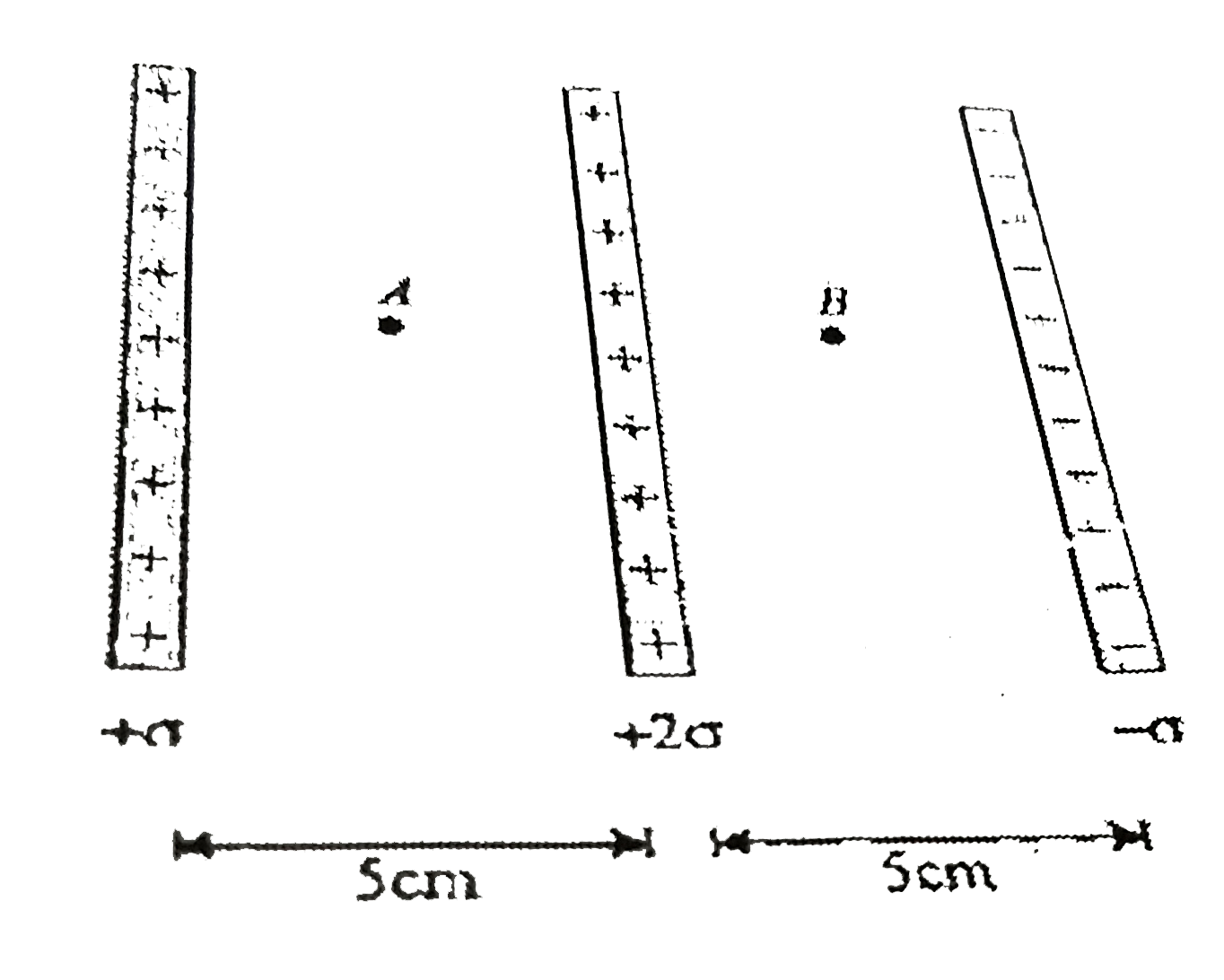
View SolutionWhat is an equipotential surface ? Write three properties Sketch equipotential surfaces of
(i) Isolated point charge
(ii) Uniform electric field
(iii) Dipole If charge Q is given to a parallel plate capacitor and E is the electric field between the plates of the capacitor the force on each plate is 1/2 QE and if charge Q is placed between the plates experiences a force equal to QE. Give reason to explain the above.
View SolutionA charge of 1μC is given to one plate of a parailel - plate capacitor of capacitance 0.1μF and a charge of 2μC is given to the other plate . Find the potential difference developed between the plate .
View SolutionA parallel plate vacuum capacitor eith plate area A and separation x has charges+Q and −Q on its plates. The capacitor is disconnected from the source of charge, so the charge on each plate remains fixed.
a. What is the total energy stored in the capacitor?
b. The plates are pulled apart an additional distance each case.
c. If F is the force with which the plates attract each other, the change in the stored energy must equal the work dW=Fdx done in pulling the plates apart. Find an expression for F
d. Energy storage in a capacitor can be limited by the maximum electric field between the plates. What is the ratio of the electric field for the series for parallel combinations?
View SolutionThe electric field between the plates of a parallel plate capacitor is E0. The space between the plates is filled completely with a dielectric. There are n molecules in unit volume of the dielectric and each molecules is like a dumb – bell of length L with its ends carrying charge +qand−q. Assume that all molecular dipoles get aligned along the field between the plates. Find the electric field between the plates after insertion of the dielectric.
View SolutionTwo large conducting plates X and Y. each having large surface area A (on one side), are placed parallel to each other as shown in figure (30-E7). The plate X ia given a charge Q whereas the other is neutral. Find (a) the surface charge dendity at the inner surface of the plates X, (b) the electric field at a point to the left of the plates, (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.

View Solution

