Figure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
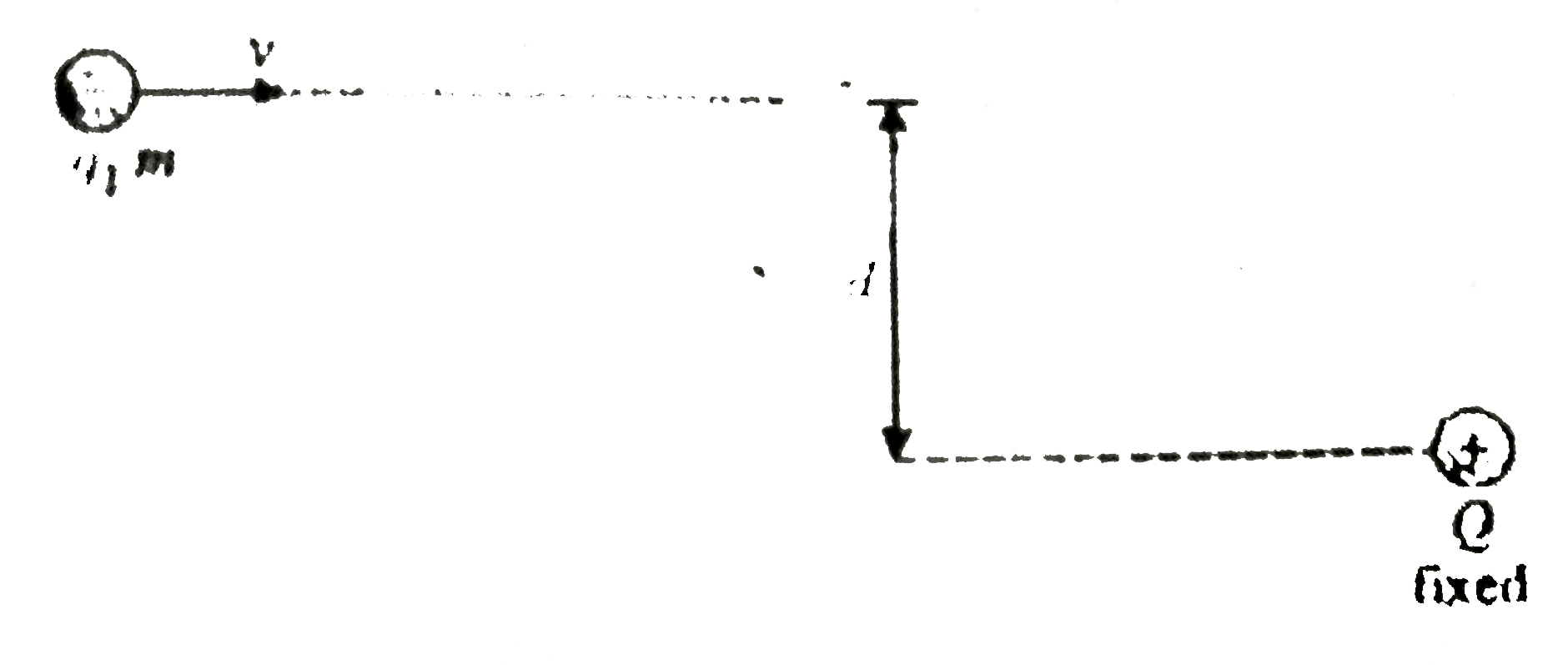
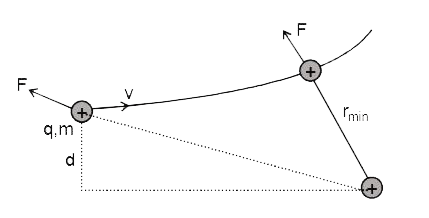
Here we can see that as +q moves toward +Q, a repulsive force acts on –q radially outward +Q. Here as the line of action of force passes through the fix charge, no torque act on +q relative to the fix point charge +Q, thus here we can say that with respect to +Q, the angular momentum of +q must remain constant. Here we can say that +q will be closest to +Q when it is moving perpendicularly to the line joining the two charges as shown.
If the closest separation in the two charges is rmin, from conservation of angular momentum we can write
mvd=mv0rmin ...(1)
Now from energy conservation, we have
12mv2=12mv20+KqQrmin
Here we use from equation (1) v0=vdrmin
12mv2=12mv2d2r2min+KqQrmin ...(2)
Solving equation (2) we'll get the value of rmin .
Topper's Solved these Questions
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 1 (Section A)
Explore 10 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 1 (Section B)
Explore 10 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:Exercise -3 Section (B) Previous Year Problems | JEE Main
Explore 30 Videos
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise - 4 (Level - II)
Explore 30 Videos
Similar Questions
A charged particle of mass m and charge q is kept initially at rest on a frictionless surface. Another charged particle of mass 4m and charge 2q starts moving with velocity v towards it. Calculate the distance of the closest approach for both the charged particles.
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
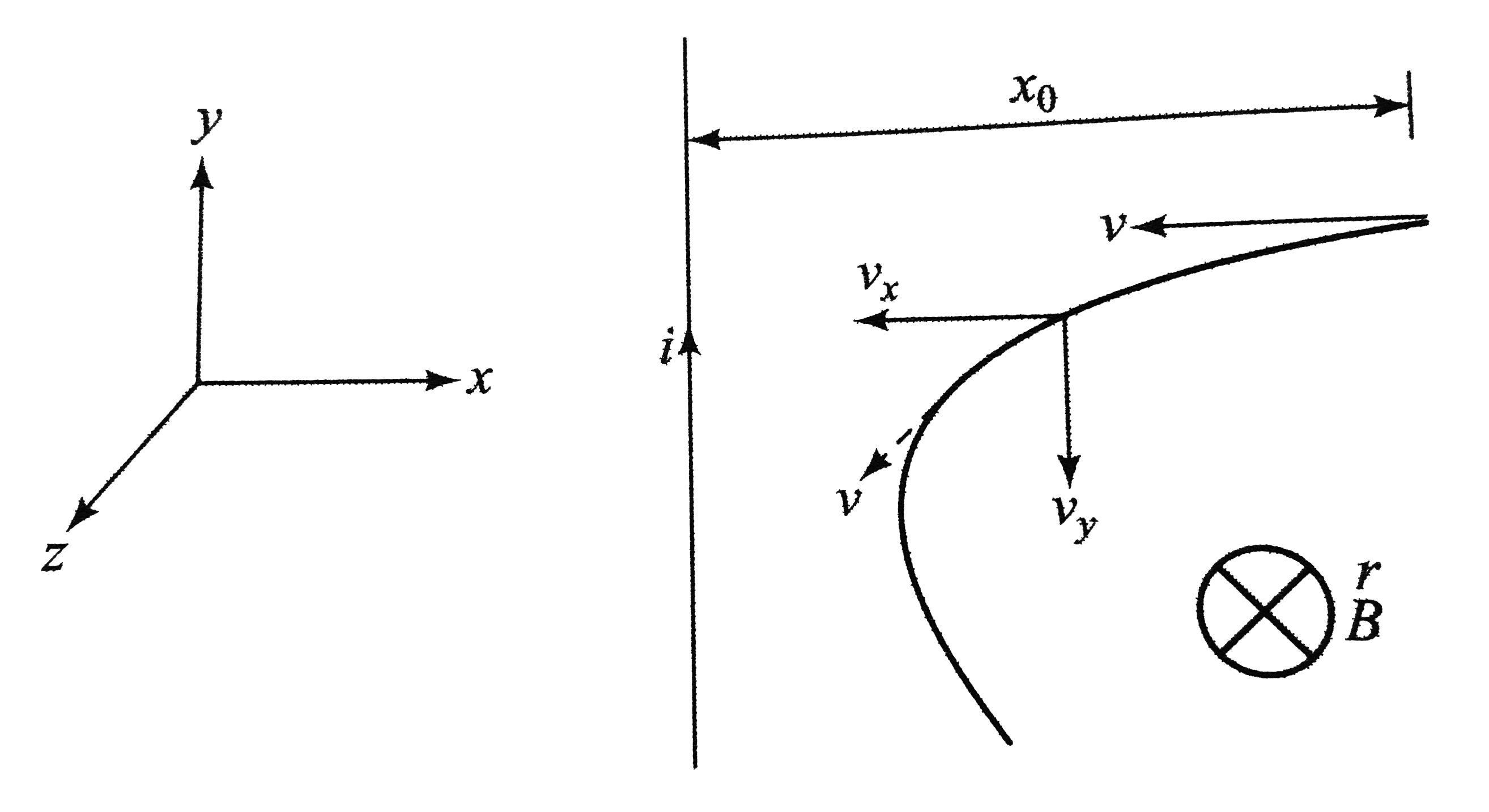

View Solution
Knowledge Check
A charge q of mass m is projected form a long distance with speed v towards another stationery particle of same mass and charge the distance of closet approach of the particles is
Aq22πε0mv2B2q2πε0mv2C3q22πε0mv2Dq2πε0mv2If and α-paricle of mass m, charged q and velocity v is incident on a nucleus charge Q and mass m, then the distance of closest approach is
AQq4πε0m2BQq2πε0mv2CQqmv22DQqmv2A charged particle q is shot from a large distance towards another charged particle Q which is fixed, with speed v. It approaches Q up to as closed distance r and then returns. If q were given a speed 2v, the distance of approach would be
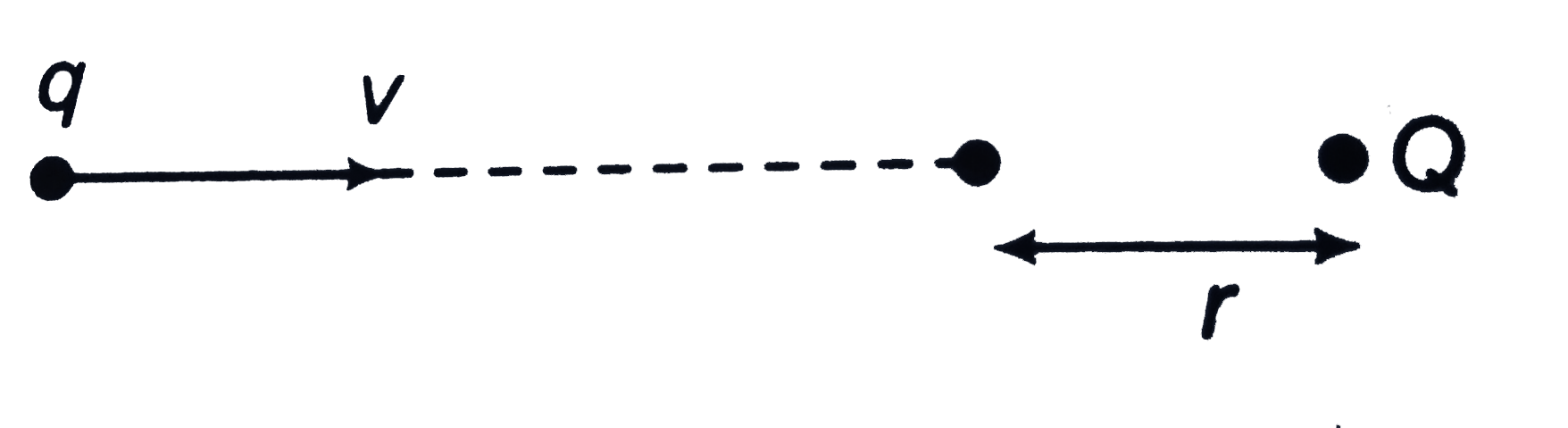 ArB2rCr/2Dr/4
ArB2rCr/2Dr/4
A proton moves from a large distance with a speed u m/s directly towards a free proton originally at rest. Find the distance of closest of closest approach for the two protons in terms of mass of proton m and its charge e.
View SolutionA particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation is
View SolutionIn the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight

View SolutionA particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation is
View SolutionA particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
What are the speeds of particles P and Q, when their separation is minimum ?
View Solution
