If →F=yˆi+xˆj then find out the work done in moving the particle from position (2, 3) to (5, 6)
dw=→F.d→s
dw=(yˆi+xˆj).(dxˆi+dyˆj)
dw=ydx+xdy
Now ydx+xdy=d(xy) (perfect differential equation)
⇒dw=d(xy)
for total work done we integrate both side
∫dw=∫d(xy)
Put xy = k
then at (2,3) ki=2×3=6
at (5,6)kf=5×6=30
then w=∫306dk=[k]306
⇒w=(30−6)=24 Joule
Topper's Solved these Questions
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)
10 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)
10 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)
30 Videos
Similar Questions
If →F=yˆi+xˆj then find out the work done in moving the particle from position (2,3) to (5,6)
View SolutionA particle moves on a circular path of radius R under the action of two constant forces F1andF2.F1 act along positive x axis and F2 acts along positive y-axis. Find the work done by F1andF2 in moving the particle from position A to position B as shown in figure.
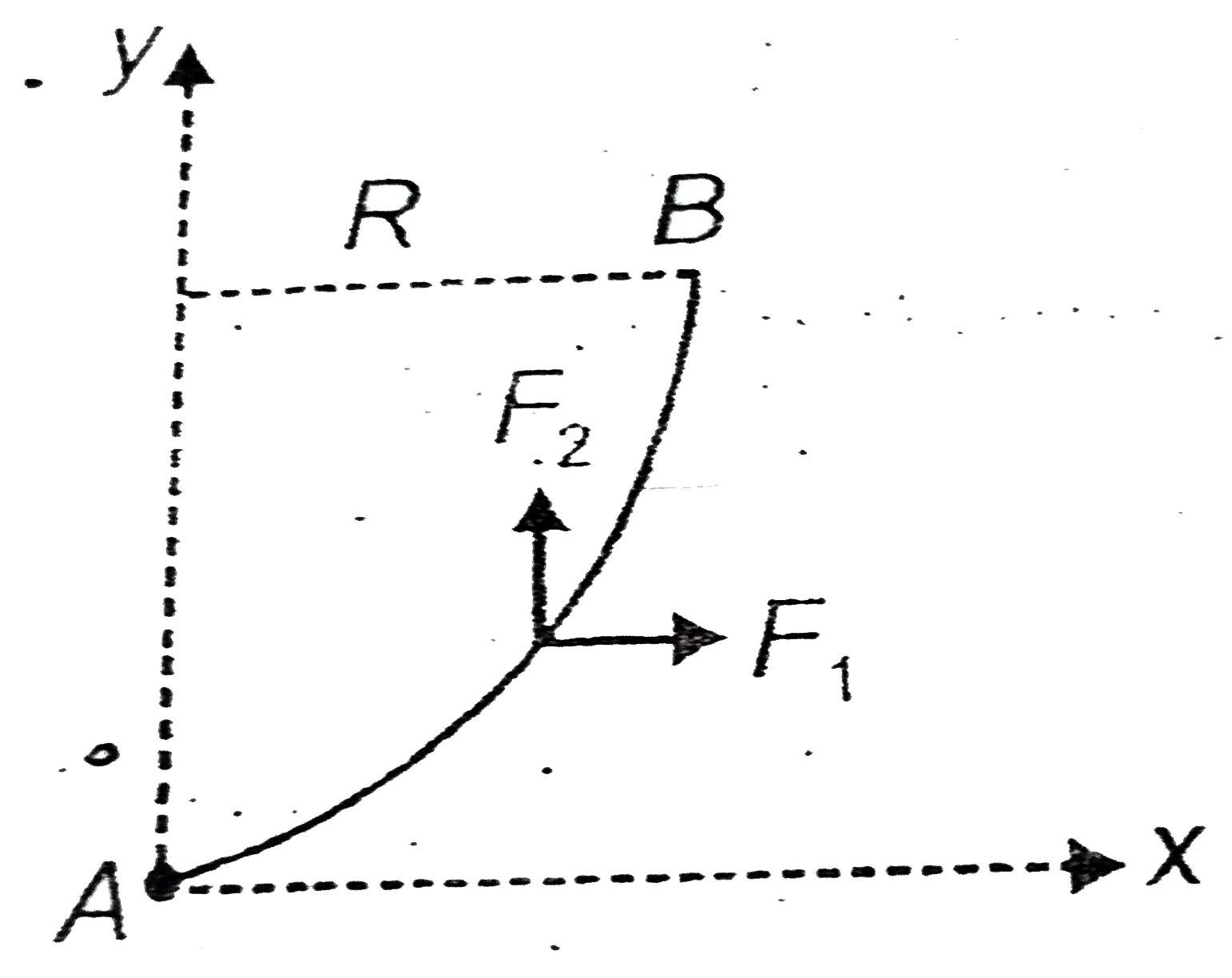
View Solution
Knowledge Check
When work done on a particle is positive, then its
AKE increasesBKE decreasesCKE remains constantDmomentum increasesParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
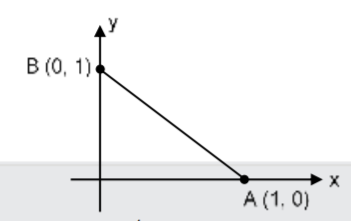 A1 JB1/2 JC2 JD3 J
A1 JB1/2 JC2 JD3 JA particle constrained to move along the Y axis of a coordinate system in subject to a constant force .
→F=(5ˆi+4ˆj+3ˆk) newton.
What is the work done by this force is moving the particle throught 5 m along the Y axis ?A12 JB15 JC18 JD20 J
If force F=(2x+3x2)N is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
View Solution(a) A particle is acted upon by a force →F given by →F=Acosωtˆi+Bˆk and its position vector →r=a[(cos)(ωt)ˆi+sin(ωt)ˆj]+12bt2ˆk. Find the work done on the particle by the force →F from time t=π/2ω to time t=π/ω.
(b) A particle moves under a force →F=xyˆi+y2ˆj and traverses along a path y=4x+1. Find the work done by the force when the particle is displaced from the point P(1, 5) to Q(2, 9).
View SolutionThe force on a particle is directed along an x axis and given by F=F0(x/x0−1). Find the work done by the force in moving the particle from x=0 to x=2x0 by (a) plotting F(x) and measuring the work from the graph and (b) integrating F(x).
View SolutionA particle moves from a point →r2=(2ˆi+3ˆj) to another point →r2=(3ˆi+2ˆj) during which a certain force →F=(5ˆi+5ˆj) acts on it. Calculate work done by the force on the particle during this displacement.
View SolutionA force F=(3xˆi+4ˆj) Newton (where x is in metres) acts on a particle which moves from a position (2m, 3m) to (3m, 0m). Then the work done is
View Solution
