A thin fixed of radius 1 metre has a positive charge 1×10−5 coulomb uniformly distributed over it. A particle of mass 0.9 gm and having a negative charge of 1×10−6 coulomb is placed on the axis at a distance of 1cm from the centre of the ring. Show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations.
Let us first find the force on a – q charge placed at a distance x from centre of ring along its axis. Figure shows the respective situation.
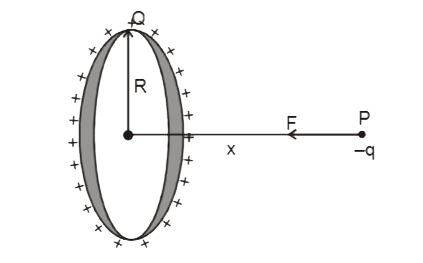
In this case force on particle P is
FP=−qE=−qKQx(x2+R2)3/2
For small x, x<<R, we can neglect x, compared to R, we have
F=KqQxR3
Acceleration of particle is a=−KqQmR3x ,
[Here we have x = 1 cm and R = 1 m hence x<<R can be used ]
This shows that particle P excutes SHM, now comparing this acceleration with a=−ω2x
ω=√KqQmR3
Thus time period of SHM is T
=2πω=2π√mRKqQ=2π√0.9×10−3×(1)39×109×10−5×10−6
π5 seconds
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)10videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)10videos
ELECTROSTATICS - I
- BOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main30videos
ELECTROSTATICS
- BOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)30videos
ELECTROSTATICS-II
Similar Questions
A thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.
 View Solution
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View Solution
Knowledge Check
- Question 1 - Select One
A non conducting spherical shell of diameter 10 cm has a charge of 1.6×10−4C. A charge of 20 C is placed at a distance of 10 cm from its centre, then force between them will be :-
A4×109NB16×1015NC3×109ND6×10−9N - Question 2 - Select One
A semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
A27 VB13.5 VC54 VD45.5 V - Question 3 - Select One
The electronic charge is 1.6×10−19 coulomb. If a body carries a negative charge of 9.6×10−10 coulombs, what is the number of excess electrons on the body?
A6×109B1/6×10−29C6×1029D6×1029
Mass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a ismple harmonic motion along the axis of the ring.
View SolutionA charge +Q is uniformly distributed over a thin ring of a radius R. Find the velocity of a negative point charge -Q at the moment it passes through the centre of the ring if it was initially at rest at infinity on the axis of the ring. The mass of the charge-Q is equal to m.
View SolutionA conducting ring of radius 40 cm has a charge of 5×10−9 C uniformly distributed over it. Calculate the electric field intensity at a point P, 40 cm away from the centre on the axis of the ring.
View SolutionA charge +Q is uniformluy distributed over a thin ring with radus R.a negative point charge -Q and mass m starts from rest at a pont far away from the centre of the ring and moves towardsn then centre. Find the velocity of this particle at the moment it passes through the centre of the ring .
View Solution

