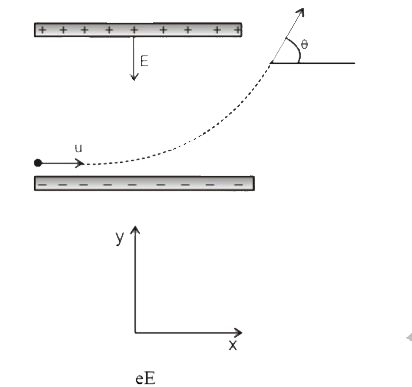
A uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

The situation is shown in figure. Here we know in X-direction speed of electron remains uniform In X direction
uX=u
In Y direction Vy initial=0
Acceleration in y-direction of electron is
a=eEm
VYfifnal =uYintial+at
Vy=(eEm)(lu)
tanθ=VyVx=eElmu/u
θ=tan−1(eElmu2)
Topper's Solved these Questions
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)
10 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)
10 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)
30 Videos
Similar Questions
A uniform electric field E=91×10−6V/m is created between two parallel, charged plates as shown in figure. An electron enters the field symmetrically between the plates with a speed v0=4×103m/s. The length of each plates is l=1m. Find the angle of deviation of the path of the electron as it comes out of the field. (Mass of the electron is m=9.1×10−31kg and its charge is e=−1.6×10−19C).

View SolutionA uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan−1(eElμ2)]

View Solution
Knowledge Check
For uniform electric field, potential difference between the plate is
A1ε0QAdB1ε0AdQCε0QAdD1ε0QdAThe electric field (→E) between two parallel plates of a capacitor will be uniform if.
Athe plate separation (d) is equal to area of the plate (A)Bthe plate separation (d) greater when compared to area of the plate (A)Cthe plate separation (d) is less when compared to area of the plate (A)D2 (or) 3A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircle
A stream of electrons moving with a velocity of 3×107ms−1 is deflected by 2 mm in traversing a distance of 0.1 m in a uniform electric field of strength 18Vm−1 in Fig. 1.42. An electron enters the field symmetrically between the plates with a speed υ0. The length of each plate is l. Find the angle of deviation of the bath of the electron as it comes out of the field.
View SolutionA uniform electric field 'E' exists between two parallel plates having opposite having opposite charge on each plates. An electron enters the field between the plates with speed v0 as shown in the figure. If length of each plate is l then angle with which electron deviates from its initial path is (m is mass of electron ) (##AAK_TST_05_NEET_YEAR(19)_PHY_E05_133_Q01##)
View SolutionA uniform electric field E axis between two charged plates as shown in Fig. What would be work done in moving a charge q along the closed recetangualr path ABCDA ?
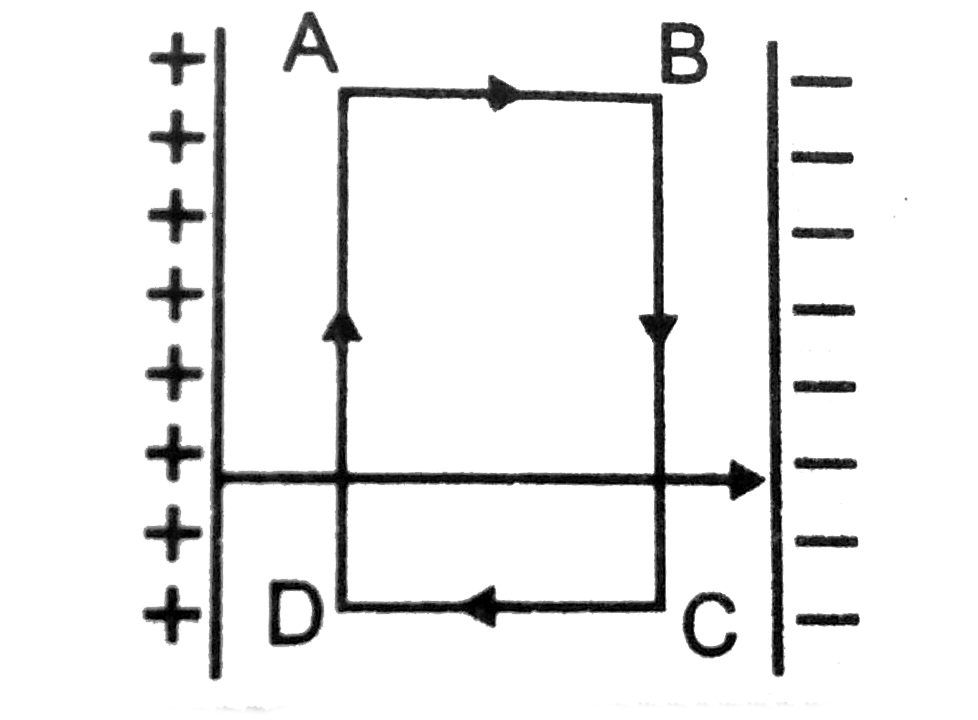
View SolutionA proton of mass m and accelerated by a potential difference Vgets into a uniform electric field of a parallel plate capacitor parallel to plates of length 1 at mid-point of its separation between plates. The field strength in it varies with time as E = at, where a is a positive constant. Find the angle of deviation of the proton as it comes out of the capacitor. (Assume that it does not collide with any of the plates.)
View SolutionAn electric field of intensity E is set up between two parallel plates of length L. An electron beam enters the field at an angle α>0 to the plates and leaves it at an angle β<0 (Fig.). Find the initial velocity of the electrons. The force of gravity is to be neglected.
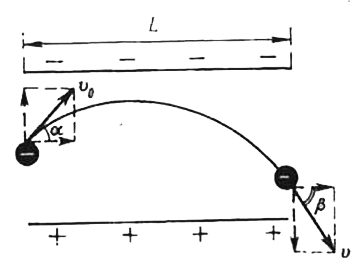
View Solution
