Two sources $S_{1} and S_{2}$ separated 2.0 m, vibrate according to equation $y_{1} = 0.03 sin π t and y_{2} = 0.02 sin π t where y_{1}, y_{2}$ and t are in M.K.S unit. They send out waves of velocity 1.5 m/s. Calculate the amplitude of the resultant motion of the particle co-linear with $S_{1} and S_{2}$ and located at a point
In the middle of $S_{2} and S_{2}$ .

Video Solution

Text Solution

Verified by Experts

The situation of shown in figure

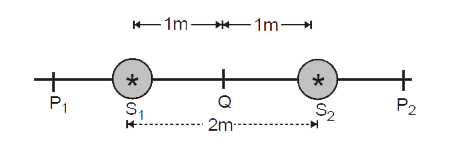
The oscillations $y_{1} and y_{2}$ have amplitudes $A_{1} = 0.03 m and A_{2} = 0.02$ respectively.
The frequency of both sources in $n = \frac{ω}{2 π} = \frac{1}{2} = 0.5 H z$ .
Now wavelength of each wave $λ = \frac{v}{n} = \frac{1.5}{0.5} = 3.0 m$
For a point Q, between $S_{1} and S_{2}$ the path difference is zero i.e., $ϕ = 0$ . Hence costructive interference take place at Q, thus amplitude at this point is maximum and given as
$R = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2}}$
$= A_{1} + A_{2} = 0.03 + 0.02 = 0.05$ m.

Updated on:21/07/2023

A particles executes SHM according to the equation y = 2 sin $2 π t$ , where y is displacement in m and t is time in s. The distance covered by the particle in 4 s of its motion is
A0
B2 m
C8 m
D32 m
The equation of progressive wave is $y = 0.2 sin 2 π$ $[\frac{t}{0.01} - \frac{x}{0.3}]$ , where x and y are in metre and t is in second. The velocity of propagation of the wave is
A30 m/s
B40 m/s
C300 m/s
D400 m/s
Two parallel S.H.M.s have equations $y_{1} = A_{1} sin (ω t + 2 π)$ and $y_{2} = A_{2} sin (\frac{ω}{t} + 4 π)$ . The amplitude of the resultant motion is
A $+ = (A_{1} + A_{2})$
B $+ = (A_{1} - A_{2})$
C $\sqrt{A_{1}^{2} + A_{2}^{2} + A_{1} A_{2}}$
D $\sqrt{A_{1}^{2} + A_{2}^{2}}$