A tube of a certain diameter and of length $48 c m$ is open at both ends. Its fundamental frequency is found to be $320 H z$ . The velocity of sound in air is $320 m / sec$ . Estimate the diameter of the tube.
One end of the tube is now closed. Calculate the lowest frequency of resonance for the tube.

Video Solution

Text Solution

Verified by Experts

The displacement curves of longitudial waves in a tube open at both ends is shown in figure (a) and (b).

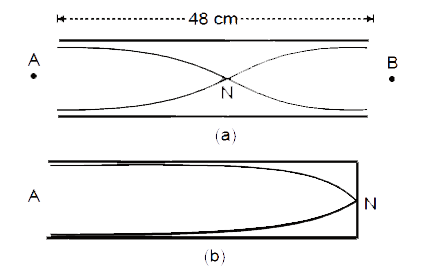
Let r be the radius of the tube. We know the antinodes occur slightly outside the tube at a distance 0.6 r from the tube end.
The distance between two antinodes is given by
$\frac{λ}{2} = 48 + 2 \times 0.6 r$
We have $λ = \frac{v}{n} = \frac{32000}{320} = 100$ cm
or $50 = 48 + 1.2 r$
or $r = \frac{2}{1.2} = 1.67$ cm
Thus diameter of the tube is $D = 2 r = 3.33$
When one end is closed, then
$\frac{λ}{4} = 48 + 0.6 r = 48 + 0.6 \times 1.67 = 49$
or $λ = 4 \times 49 = 196$ cm
Now $n = \frac{v}{n} = \frac{32000}{196} = 163.3$ Hz.

Updated on:21/07/2023

A tube of diameter $d$ and of length $l$ unit is open at both ends. Its fundamental frequency of resonance is found to be $v_{1}$ . The velocity of sound in air is $330 m / sec$ . One end of tube is now closed. The lowest frequency of resonance of tube is now $v_{2}$ . Taking into consideration the end correction, $\frac{v_{2}}{v_{1}}$ is

A $\frac{(l + 0.6 d)}{(l + 0.3 d)}$
B $\frac{1 (l + 0.3 d)}{2 (l + 0.6 d)}$
C $\frac{1 (l + 0.6 d)}{2 (l + 0.3 d)}$
D $\frac{1 (d + 0.3 l)}{2 (d + 0.6 l)}$
If the end correction of an open tube is 0.3 cm, then the diameter of the tube will be
A1cm
B0.3cm
C0.5cm
D3cm
What is minimum length of a tube, open at both ends, that resonates with tuning fork of frequency 350 Hz ? [velocity of sound in air = 350 m/s ]
A $50 c m$
B $100 c m$
C $75 c m$
D $25 c m$