The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is
4 units.
6 units.
8 units.
10 units
The correct Answer is:D
To find the moment of inertia (M.I.) of a disc about an axis through a point on its rim and in the plane of the disc, we can follow these steps:
Step 1: Understand the Given Information
We know that the moment of inertia of the disc about its diameter (Id) is given as 2 units. The formula for the moment of inertia of a disc about its diameter is:
Id=14mr2
Step 2: Calculate the Mass Moment of Inertia
Since we have Id=2 units, we can express this in terms of mass (m) and radius (r):
14mr2=2
From this, we can find mr2:
mr2=8(1)
Step 3: Use the Perpendicular Axis Theorem
According to the perpendicular axis theorem, for a planar body, the moment of inertia about an axis perpendicular to the plane of the body (Iz) is the sum of the moments of inertia about two perpendicular axes in the plane of the body (Ix and Iy):
Iz=Ix+Iy
For a disc, both Ix and Iy are equal to Id:
Iz=2Id
Step 4: Apply the Parallel Axis Theorem
Now, we need to find the moment of inertia about an axis through a point on its rim (Ir). We can use the parallel axis theorem, which states:
Ir=Icm+md2
Where:
- Icm is the moment of inertia about the center of mass (which is Id),
- d is the distance from the center of mass to the new axis (which is equal to the radius r of the disc).
Step 5: Substitute Values
From the previous steps, we know:
- Icm=Id=14mr2=2 units
- d=r
Thus, we can write:
Ir=Id+mr2
Substituting Id=2 and using equation (1) where mr2=8:
Ir=2+8
Step 6: Calculate the Final Moment of Inertia
Now, we can calculate:
Ir=10 units
Final Answer
The moment of inertia of the disc about an axis through a point on its rim and in the plane of the disc is 10 units.
---
We know that the moment of inertia of the disc about its diameter (Id) is given as 2 units. The formula for the moment of inertia of a disc about its diameter is:
Since we have Id=2 units, we can express this in terms of mass (m) and radius (r):
According to the perpendicular axis theorem, for a planar body, the moment of inertia about an axis perpendicular to the plane of the body (Iz) is the sum of the moments of inertia about two perpendicular axes in the plane of the body (Ix and Iy):
Now, we need to find the moment of inertia about an axis through a point on its rim (Ir). We can use the parallel axis theorem, which states:
- Icm is the moment of inertia about the center of mass (which is Id),
- d is the distance from the center of mass to the new axis (which is equal to the radius r of the disc).
From the previous steps, we know:
- d=r
Now, we can calculate:
The moment of inertia of the disc about an axis through a point on its rim and in the plane of the disc is 10 units.
Topper's Solved these Questions
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 2 (Level -I)
Explore 51 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 2 (Level - II)
Explore 25 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Example 31
Explore 1 Video
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 4 (LEVEL - II)
Explore 14 Videos
Similar Questions
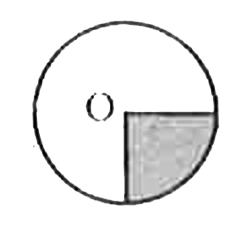
The M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is MR22 . If one quarter of the disc is removed, the new moment of inertia of the disc will be
View SolutionM.I. of a thin uniform circular disc about one of the diameters is I. Its M.I. about an axis perpendicular to the plane of disc and passing through its centre is
View Solution
Knowledge Check
The M.I. of a uniform disc about a diameter is I. Its M.I. about an axis perpendiçular to its plane and passing through a point on its rim is
A51B61CID4IThe M.L. of a uniform disc about the diameter is 1. Its M.I. about an axis perpendicular to its plane and passing through a point on its rim is
A4IB5IC6IDIThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
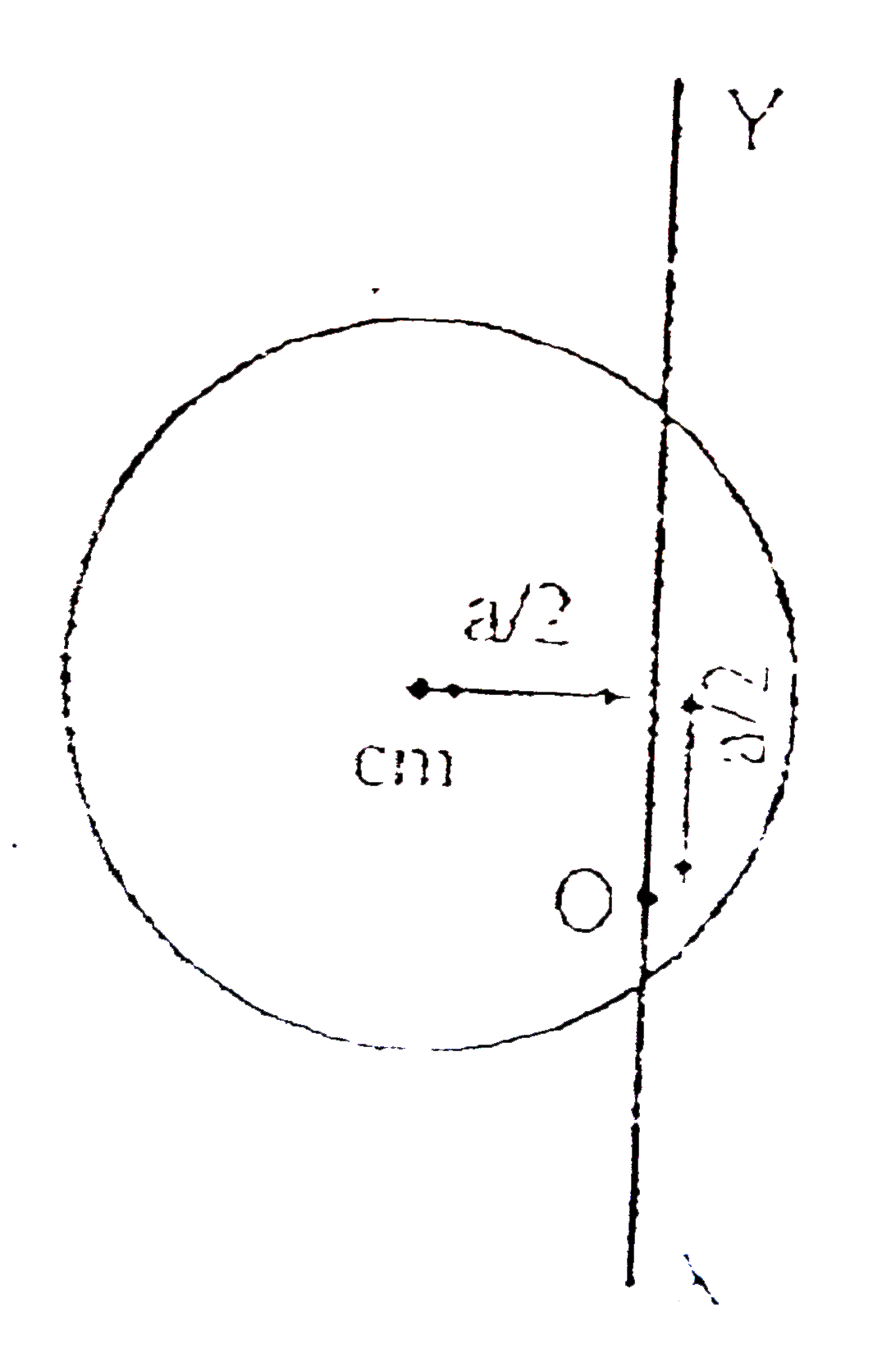 A43Ma2BI+14Ma2C2IDI2
A43Ma2BI+14Ma2C2IDI2
Consider the following statements.
I. MI of a disc about any diameter =14MR2
II. MI of a ring about an axis perpendicular to its face and passing through its rim =32MR2. Choose the correct option.
View SolutionA disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View SolutionFour particles each of mass m are lying symmetrically on the rim of a disc of mass M and radius R. Moment of inertia of this system about an axis passing through one of the particles and I to plane of disc is
View SolutionMoment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionMoment of inertia (M.I.) of four bodies, having same mass and radius, are reported as ,
I1 = M.I. of thin circular ring about its diameter.
I2 = M.I. of circular disc about an axis perpendicular to the disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter. Then :
View Solution

