The ladder shown in figure has negligible mass and rests on a frictionless floor. The crossbar connects the two legs of the ladder at the middle. The angle between the two legs is 600. The fat person sitting on the ladder thas a mas of 80 kg. Find the contact force exerted by the floor on each leg and the tension in the cross bar.
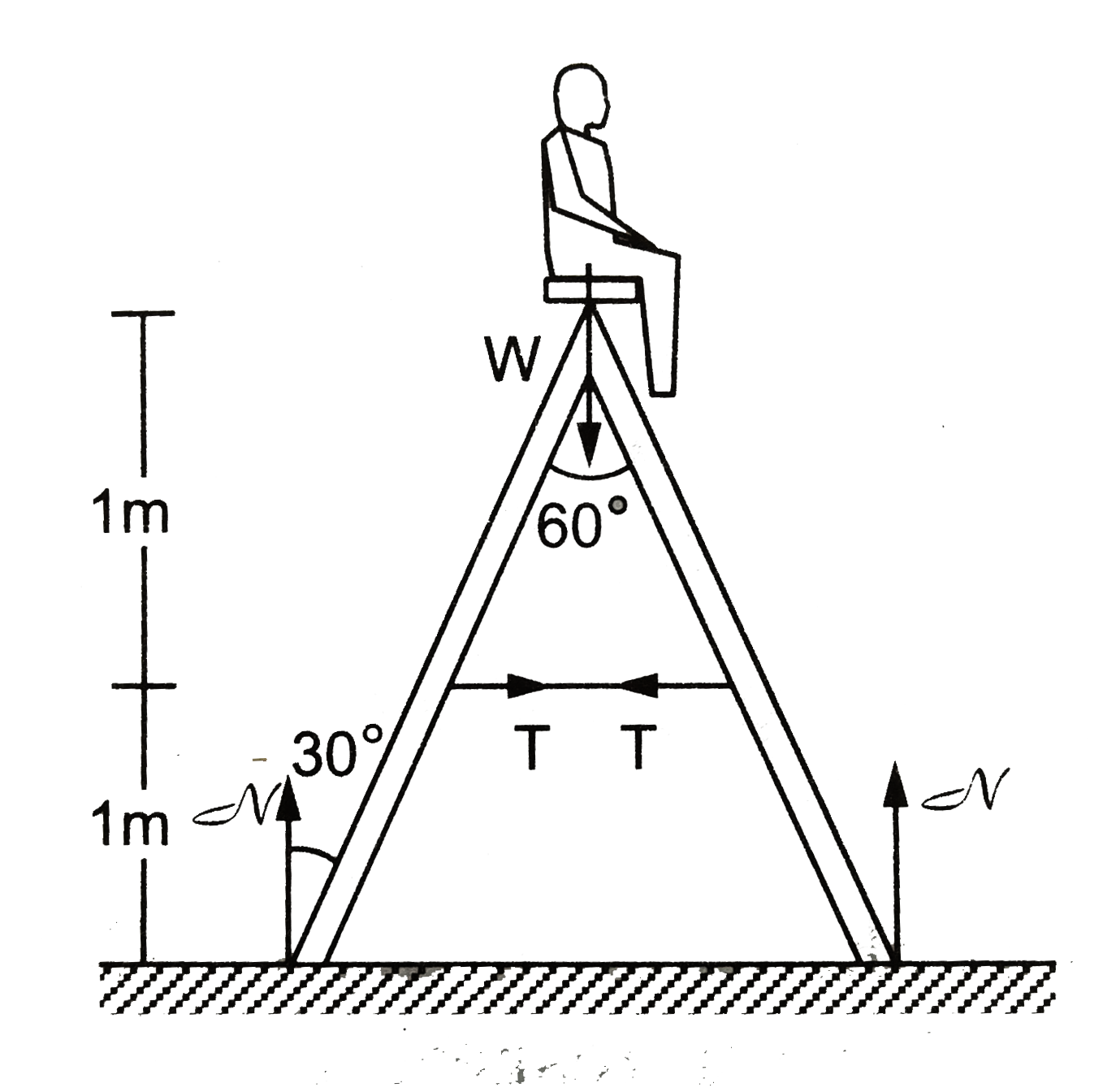
The forces acting on different parts are shown in figure. Consider the vertical equilibrium of the ladder plus the person system . The forces acting on this system are its weight (80 kg) g and the contact force N + N = 2 N due to the floor. Thus 2N = (80 kg) g or N = (40 kg) (9.8m/s2)=392 N
Next consider the equilibrium of the left leg of the ladder. Taking torques of the forces acting on it about the upper end,
N(2m)tan30∘=T(1m)
or T=N2√3=(392N)×2√3=450N
Topper's Solved these Questions
Similar Questions
A ladder of mass 10 kg is resting with its top end touching a vertical wall and the bottom end on the floor. If the angle between the ground and the ladder is 45°, find the horizontal force required at the bottom to prevent the ladder from sliding. Neglect friction and take g=10ms−2.
View SolutionA rubber ball of mass 0⋅4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0⋅4 s, find the average force exerted by the ball on the ground .
View Solution
Knowledge Check
Two blocks of masses 40 kg and 20 kg are connected by a wire that has a linear mass density of 1g/m. These blocks are being pulled across horizontal frictionless floor by horizontal force F that is applied to 20 kg block. A transverse wave travels on the wave between the blocks with a speed of 400m/s (relative to the wire). the lmass of the wire is negligible compared to the mass of the blocks. the magnitude of F is
A160 NB240 NC320 ND400 N
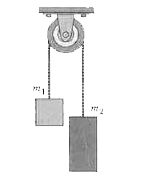
Figure 5-50 shows two blocks connected by a cord (of negligible mass) that passes over a frictionless pulley (also of negligible mass). The arrangement is known as Atwood's machine. One block has mass m1=1.30 kg, the other has mass m2=2.80 kg. What are (a) the magnitude of the blocks' acceleration and (b) the tension in the cord ?
View SolutionA uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.

View SolutionA 3 m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in the following figure, Find the reaction forces of the wall and the floor.
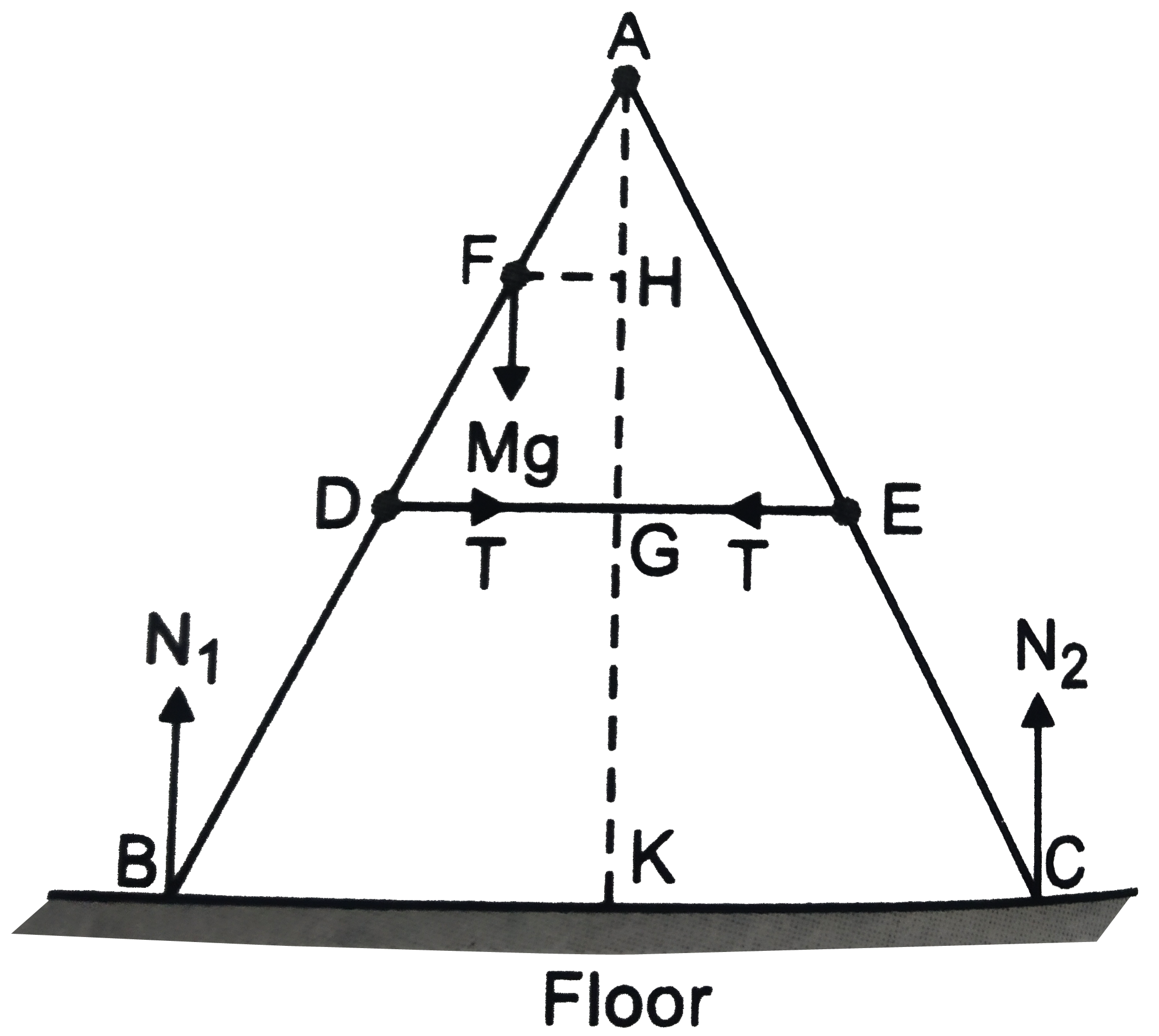
View SolutionThe step-ladder shown in figure 6.11 is 8 m long and hinged at C.BD is a tie rod 2.5 m long half way up. A man of 86 kg climbs 6 m along the ladder . Find the tension in the tie rod the forces exerted on the ladder by the assuming the floor to frictionless and the ladder weightless.

[Hints: Consider the free-body diagram of the sides of the ladder.]
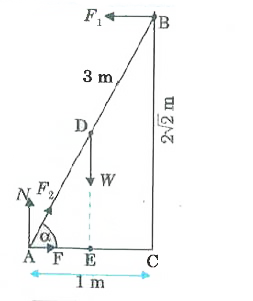
View SolutionAs shown in Fig. the two sides of a step ladder BA and CA are 1.6m long and hinged at A. A rope DE,0.5m is tied half way up. A weight 40kg is suspended from a point F,1.2m from B along the ladderBA. Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g=9.8m/s2)
(Hint. Consider the eqilibrium of each side of the ladder separately.)
View SolutionA ladder of length 6 metres makes an angle of 45∘ with the floor while leaning against one wall of a room. If the foot of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60∘ with the floot. Find the distance between two walls of the room.
View SolutionTwo blocks are kept in contact as shown in figure. Find ( a) forces exerted by surfaces ( floor and wall ) on blocks ( b) contact force between two blocks.
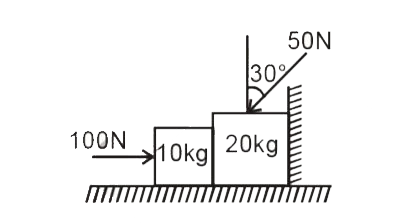
View Solution
