
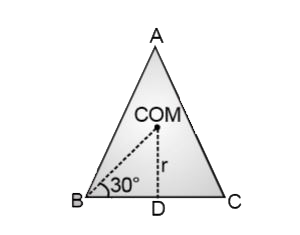
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.
Moment of inertia of rod BC about an axis perpendicular to plane of triangle ABC and passing through the mid-point of rod BC (i.e., D) is
I1=ml212
From theorem of parallel axes, moment of inertia of this rod about the asked axis is
I2=I2+mr2=ml212+m(l2√3)2=ml26
∴ Moment of inertia of all the three rod is
I=3I2=3(3l26)=ml22
Topper's Solved these Questions
Similar Questions
Three particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View SolutionFour thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View Solution
Knowledge Check
Two uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
AMl212BMl26CMl24DML23Two rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
Aml2/12Bml2/6Cml2/3Dml2/2Two rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
Aml2/12Bml2/6Cml2/3Dml2/2
Two point masses m1 and m2 are joined by a weightless rod of length r. Calculate the moment of inerrtia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionThree particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
View SolutionFour thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View SolutionFour thin rods same mass M and same length l, from a square as shown in figure. Moment of inertia of this system about an axis passing through one corner of the square and perpendicular to its plane is

View Solution
