A long plank begins to move at and accelerates along a straight track wit a speed given by for (where is in m/s and is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at sec and stops sliding at sec. If the coefficient of static friction and kinetic friction between the plank and the block is and (where and are digits) respectively, find (take )
The correct Answer is:
Step by step video, text & image solution for A long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t^(2) for 0le t le 2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-I)13videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)15videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-3(Level-I)18videos
NLM & FRICTION
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B12videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN12videos
ONE DIMENSION MOTION
Similar Questions
A long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t2 for 0≤t≤2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m/s2)
View SolutionA car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png) View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
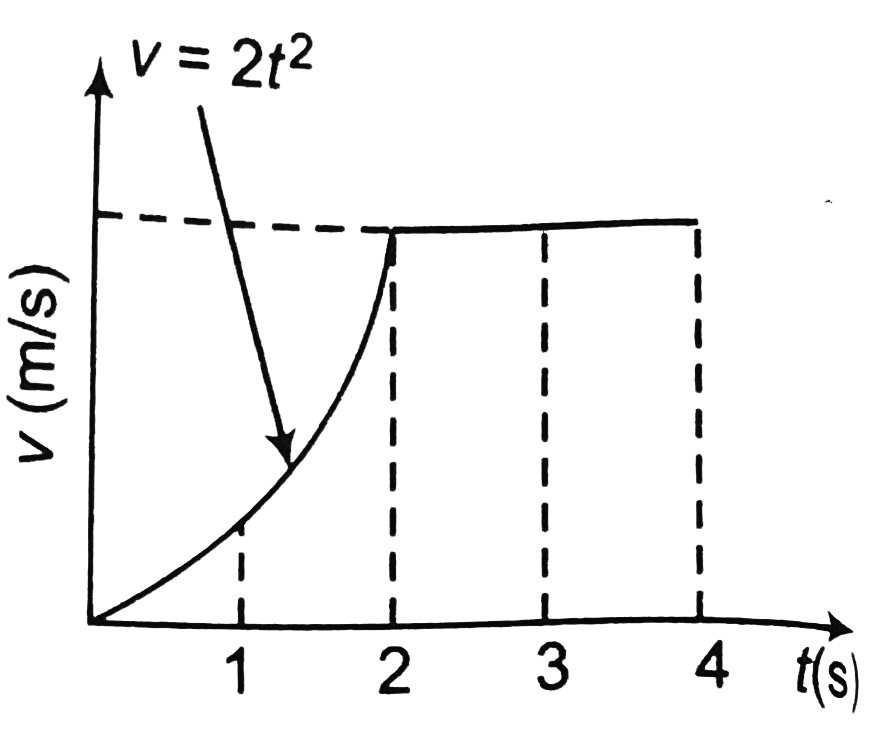 A0.2B0.3C0.4D0.5
A0.2B0.3C0.4D0.5 - Question 2 - Select One
The velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2) - Question 3 - Select One
The displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
A2m/s2B4m/s2C6m/s2D8m/s2
The speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionIf a particle moves in a circle of radius 4m at speed given by v = 2t where v is in m/s and t in sec at t = 4sec, acceleration of particle will be
View SolutionThe position of the particle moving along x-axis is given by x=2t−3t2+t3 where x is in mt and t is in second.The velocity of the particle at t=2sec is
View SolutionA car moves along a straight line whose equation of motion is given by
s=12t+3t2−2t3
where s is in metres and t is in seconds. The velocity of the car at start will be :-View Solution

