Heat is being supplied at a constant rate to a sphere of ice which is melting at the rate of 0.1 gm/sec. It melts completely in 100 sec. The rate of rise of temperature thereafter will be (Assume no loss of heat)
0.8.°C/sec
5.4.°C/sec
3.6.°C/sec
will change with time
The correct Answer is:A
To solve the problem, we need to determine the rate of rise of temperature of the water after the ice has completely melted. Here’s a step-by-step solution:
Step 1: Calculate the total mass of ice melted
The problem states that the ice melts at a rate of 0.1 grams per second for 100 seconds.
Total mass of ice melted=melting rate×time=0.1g/s×100s=10g
Step 2: Determine the heat required to melt the ice
The heat required to melt ice can be calculated using the formula:
Q=m×Lf
where:
- Q is the heat required,
- m is the mass of ice (10 g),
- Lf is the latent heat of fusion of ice, which is approximately 334J/g.
Calculating the heat required:
Q=10g×334J/g=3340J
Step 3: Determine the rate of heat supplied
Since the heat is supplied at a constant rate, we can find the rate of heat supplied (dQdt):
dQdt=Qtime=3340J100s=33.4J/s
Step 4: Calculate the rate of rise of temperature after melting
After the ice has melted, the heat supplied will now raise the temperature of the resulting water. We can use the formula:
dQdt=m×c×dTdt
where:
- c is the specific heat capacity of water, approximately 4.18J/g°C,
- m is the mass of water (10 g).
Rearranging the formula to find dTdt:
dTdt=dQdtm×c
Substituting the known values:
dTdt=33.4J/s10g×4.18J/g°C=33.441.8≈0.8°C/s
Final Answer
The rate of rise of temperature thereafter will be approximately 0.8°C/s.
---
The problem states that the ice melts at a rate of 0.1 grams per second for 100 seconds.
The heat required to melt ice can be calculated using the formula:
- Q is the heat required,
- m is the mass of ice (10 g),
- Lf is the latent heat of fusion of ice, which is approximately 334J/g.
Since the heat is supplied at a constant rate, we can find the rate of heat supplied (dQdt):
After the ice has melted, the heat supplied will now raise the temperature of the resulting water. We can use the formula:
- c is the specific heat capacity of water, approximately 4.18J/g°C,
- m is the mass of water (10 g).
The rate of rise of temperature thereafter will be approximately 0.8°C/s.
Topper's Solved these Questions
- CALORIMETRY Book:MOTIONChapter:CALORIMETRY Exercise:EXERCISE - 3 Section - A
Explore 9 Videos
- CALORIMETRY Book:MOTIONChapter:CALORIMETRY Exercise:EXERCISE - 3 Section - B
Explore 4 Videos
- CALORIMETRY Book:MOTIONChapter:CALORIMETRY Exercise:EXERCISE - 1
Explore 29 Videos
- ATOMIC STRUCTURE & X-RAY Book:MOTIONChapter:ATOMIC STRUCTURE & X-RAY Exercise:Exercise - 2
Explore 31 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
Similar Questions
Heat is being supplied at a constant rate to the sphere of ice which is melting at the rate of 0.1 gm/s. It melts completely in 100 s. The rate of rise of temperature thereafter will be
View SolutionHeat is supplied to a ice at a constant rate Temperature variation with time is as shown in figure. Then –
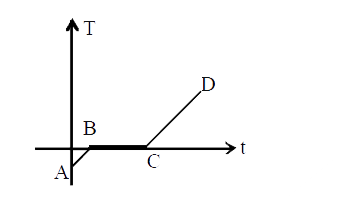
View Solution
Knowledge Check
A solid material is supplied heat at a constant rate. The temperature of material is changing with heat input as shown in the figure. What does the slope of DE represent ?
 ALatent heat of liquidBLatent heat of vaporizationCHeat capacity of vapourDInverse of heat capacity of vapour
ALatent heat of liquidBLatent heat of vaporizationCHeat capacity of vapourDInverse of heat capacity of vapourA black body at a temperature of 227∘C radiates heat energy at the rate of 5 cal/cm-sec. At a temperature of 727∘C, the rate of heat radiated per unit area in cal/cm will be
A80B160C250D500
When ice is heated the temperature of ice remains constant till it melts completely. Justify this statement.
View SolutionThe radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increases when radius is 15cm, is
View SolutionThe radius of a sphere is changing at the rate of 0.1cm/sec. The rate of change of its surface area when the radius is 200cm is
View SolutionA source of heat supplies heat at constant rate to a solid cube. The variatiion of the temperature of the cube with heat supplied is shown in figure. The portion DE of the graph represents conversion of
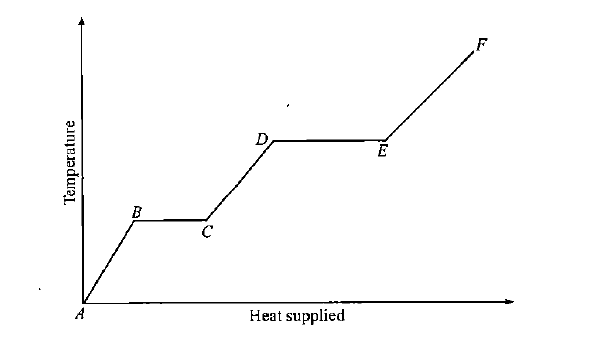
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperature. Assume that the emissivity of both the spheres is the same. Find the ratio of
(a) the rate of heat from the aluminium sphere to the rate of heat loss from the copper sphere and
(b) the rate of fall of temperature of the the aluminium sphere to the rate of fall temperature of teh copper sphere. The specific heat capacity of aluminium =900J/kg−∘C and that of copper =390J/kg−∘C. The density of copper is 3.4 times the density of aluminium.
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emissivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of all of temperature of the copper sphere. The specific heat capacity of aluminium =900Jkg−1^(@)C^(-1).andtˆofcopper=390Jkg^(-1)^(∘)C−1 . The density of copper =3.4 times the correct wattage.
View Solution