Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenuse is and the opposite vertex is the point
7y – x – 12 = 0 and 7x + y = 16.
7y + x – 12 = 0 and 7x + y = 16
7y + x – 12 = 0 and 7x – y = 16.
7y – x + 12 = 0 and 7x – y = 16.
The correct Answer is:A
Step by step video, text & image solution for Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3 x + 4 y = 4 and the opposite vertex is the point (2,2). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 2 (Level-I) DISTANCE OF A POINT FROM A LINE
2 Videos
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 2 (Level-I) POSITION OF A POINT W.R.TO A LINE
2 Videos
- STRAIGHT LINE BOOK - MOTIONCHAPTER - STRAIGHT LINE EXERCISE - Exercise 2 (Level-I) VARIOUS FORMS OF STRAIGHT LINE
8 Videos
- SOLUTION OF TRIANGLEBOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 4( LEVEL II)
10 Videos
- TANGENT & NORMALBOOK - MOTIONCHAPTER - TANGENT & NORMALEXERCISE - EXERCISE 4
14 Videos
Similar Questions
Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2,2).
View SolutionFind the equations the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View SolutionA side of an isosceles right angled triangle is x. Find its hypotenuse.
View SolutionA side of an isosceles right angled triangle is x. Find its hypotensuse.
View SolutionFind the equation of the legs of a right isosceles triangle if the equation of its hypotenuse is x−2y−3=0 and the vertex of the right angle is at the point (1,6),
View SolutionThe area of an isosceles right - angled triangle is 72 cm2 .Find its hypotenuse .
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as
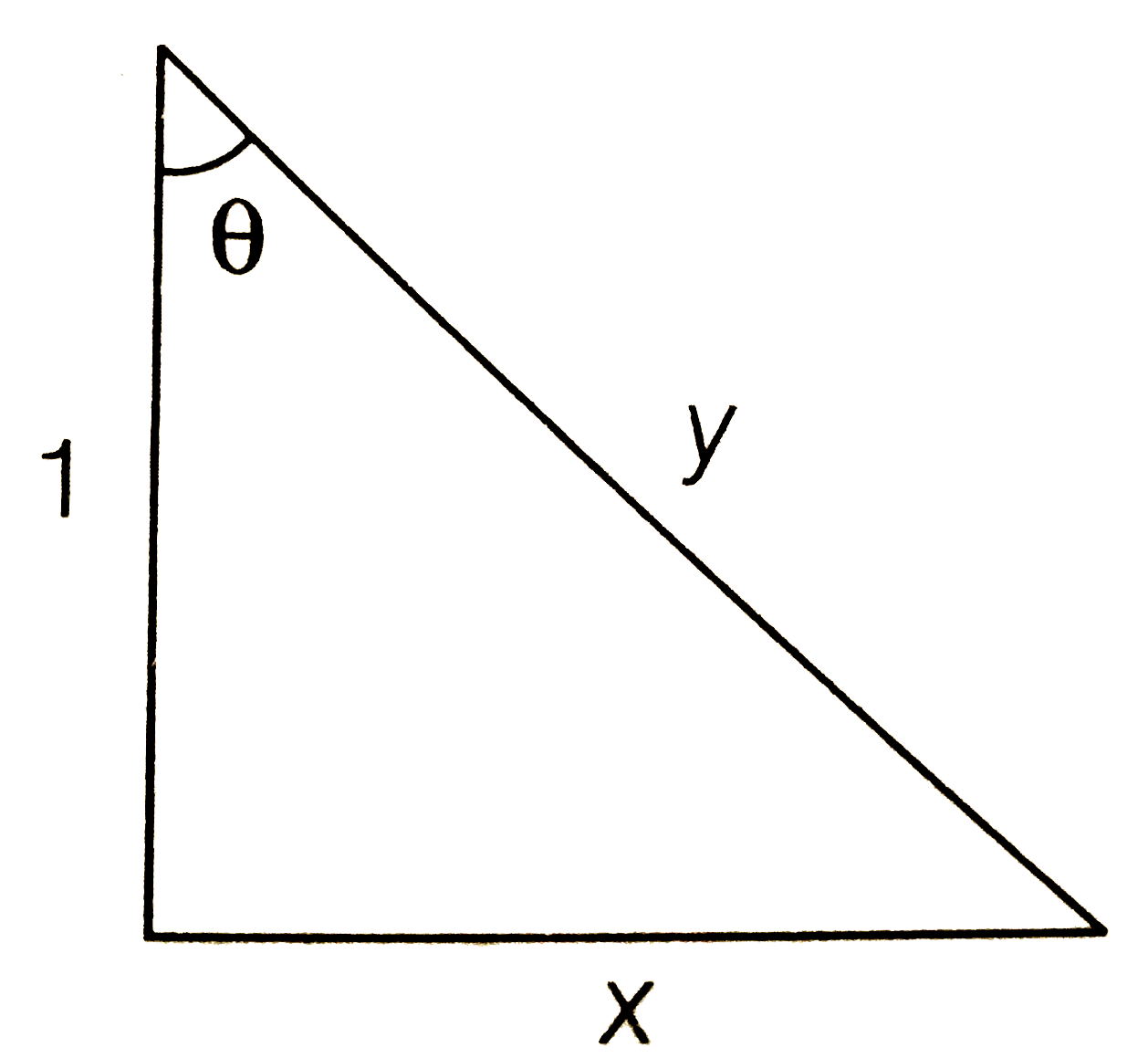

View SolutionThe area of an isosceles right triangle is 200 m^2. Find its hypotenuse.
View SolutionFind the area of an isosceles right triangle whose hypotenuse is 4√2 cm
View SolutionThe equation of the circumcircle of the triangle, the equation of whose sides are y=x,y=2x,y=3x+2, is
View Solution
