If $r_{1}, r_{2}$ be the length of the perpendicular chords of the parabola $y^{2} = 4 a x$ drawn through the vertex, then show that ${(r_{1} r_{2})}_{1}^{4 / 3} = 16 a^{2} (r_{1}^{2 / 3} + r_{2}^{2 / 3})$

Video Solution

Text Solution

Verified by Experts

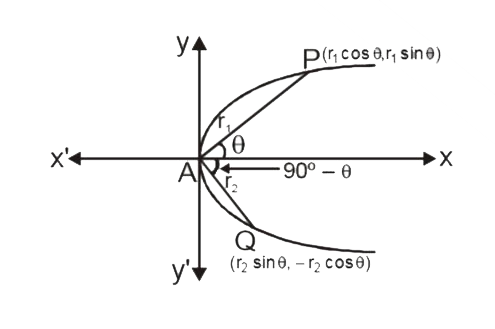
Since chord are perpendicular, therefore if one makes an angle $(90^{\circ} - θ)$ then the other will make an angle $(90^{\circ} - θ)$ with x-axis
Let $A P = r_{1}$ and $A Q = r_{2}$
If $∠ P A X = θ$ then $∠ Q A X = 90^{\circ} - θ$
$θ$ Co-ordinates of P and Q are ( $r_{1} cos θ, r_{1} sin θ$ )
and $(r_{2} sin θ, - r_{2} cos θ)$ respectively.

Since P and Q lies on $y^{2} = 4 a x$
$∴ r_{1}^{2} {sin}^{2} θ = 4 a r_{1} cos θ$
and $r_{2}^{2} {cos}^{2} θ = 4 a r_{2} sin θ$
$! r_{1} = \frac{4 a cos θ}{{sin}^{2} θ}$
and $r_{2} = \frac{4 a sin θ}{{cos}^{2} θ}$
$∴ {(r_{1} r_{2})}_{1}^{4 / 3}$
$= {(\frac{4 a cos θ}{{sin}^{2} θ} . \frac{4 a sin θ}{{cos}^{2} θ})}^{4 / 3}$
$= {(\frac{16 a^{2}}{sin θ cos θ})}^{4 / 3}$ ...(i)
and $16 a^{2} . (r_{1}^{2 / 3} + r_{2}^{2 / 3})$
$= 16 a^{2} {{(\frac{4 a cos θ}{{sin}^{2} θ})}^{2 / 3} + {((4 a sin θ) / ({cos}^{2} θ))}^{2 / 3}}$
$= 16 a^{2} . {(4 a)}^{2 / 3} {\frac{{(cos θ)}^{2 / 3}}{{(sin θ)}^{4 / 3}} + \frac{{(sin θ)}^{2 / 3}}{{(cos θ)}^{4 / 3}}}$
$= 16 a^{2} . {(4 a)}^{2 / 3} {\frac{{cos}^{2} θ + {sin}^{2} θ}{{(sin θ)}^{4 / 3}} + \frac{{(sin θ)}^{2 / 3}}{{(cos θ)}^{4 / 3}}}$
$= \frac{16 a^{3} . {(4 a)}^{2 / 3}}{{(sin θ cos θ)}^{4 / 3}}$
$= {(\frac{16 a^{2}}{sin θ cos θ})}^{4 / 3}$
$= {(r_{1} r_{2})}_{1}^{4 / 3}$ [from (i)]

Updated on:21/07/2023

|

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

A and B are two points on the parabola $y^{2} = 4 a x$ with vertex O. if OA is perpendicular to OB and they have lengths $r_{1}$ and $r_{2}$ respectively, then the valye of $\frac{r_{1}^{4 / 3} r_{2}^{4 / 3}}{r_{1}^{2 / 3} + r_{2}^{2 / 3}}$ is
A $16 a^{2}$
B $a^{2}$
C $4 a$
DNone of these

MOTION-PARABOLA-EXERCISE - IV

Home
Ask Doubt
Profile