If a tangent to the parabola y2=4ax meets the x-axis at T and intersects the tangents at vertex A at P, and rectangle TAPQ is completed, then find the locus of point Q.
Let P(at2,2at) be any point on the parabola y2=4ax. Then tangent at P(at2,2at) is ty = x + at2
Since tangent meet the axis of parabola in T and tangent at the vertex in Y.
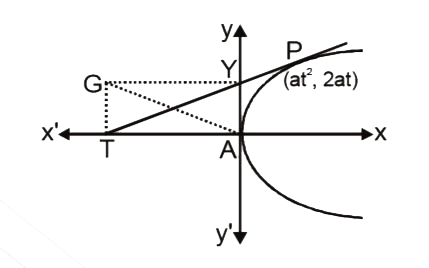
∴ Co-ordinates of T and Y are (−at2,0) and (0,at) respectively.
Let co-ordinates of G be (x1,y1).
Since TAYG is rectangle.
∴ Mid-points of diagonals TY and GA is same
!x1+02=−at2+02
!x1=−at2 ...(i)
and y1+02=0+at2
Eliminating t from (i) and (ii) then we get x1=−a(y1a) or
y21=−ax1
or y21+ax1=0
∴ The locus of G(x1,y1) is y2+ax=0
Topper's Solved these Questions
- PARABOLABOOK - MOTIONCHAPTER - PARABOLAEXERCISE - EXERCISE - I
28 Videos
- PARABOLABOOK - MOTIONCHAPTER - PARABOLAEXERCISE - EXERCISE - II
17 Videos
- MONOTONOCITYBOOK - MOTIONCHAPTER - MONOTONOCITYEXERCISE - Exercise - 4 ( Level-II ) Previous Year (Paragraph)
2 Videos
- PERMUTATION AND COMBINATION BOOK - MOTIONCHAPTER - PERMUTATION AND COMBINATION EXERCISE - EXAMPLE
23 Videos
Similar Questions
If a tangent to the parabola y2=4ax meets the x-axis at T and intersects the tangents at vertex A at P, and rectangle TAPQ is completed, then find the locus of point Q.
View SolutionIf a tangent to the parabola y2=4ax meets the axis of the parabola in T and the tangent at the vertex A in Y, and the rectangle TAYG is completed, show that the locus of G is y2+ax=0.
View Solution
Knowledge Check
if the tangent to the parabola y=x(2−x) at the point (1,1) intersects the parabola at P. find the co-ordinate of P.
A(1,2)B(1,1)C(3,-2)D(-1,-4)Tangent to the parabola y2=4ax at point P meets the tangents at vertex A at point B and the axis of parabola at T, Q is any point on this tangent and N as the foot of perpendicular from Q on SP, where S is focus, M is the foot of perpendicular from Q on the directrix then
AB bisects PTBB trisects PTCQM = SNDQM = 2SNA variable tangent to the parabola y2=4ax meets the parabola y2=−4ax P and Q. The locus of the mid-point of PQ, is
Ay2=−2axBy2=−axCy2=−43axDy2=−4ax
If a tangent to the parabola y2=4ax meets the axis of the parabola in T and the tangent at the vertex A in Y, and the rectangle TAYG is completed, show that the locus of G is Y2+ax=0.
View SolutionA tangent to the hyperbola x2−2y2=4 meets x-axis at P and y-aixs at Q. Lines PR and QR are drawn such that OPRQ is a rectangle (where O is origin).Find the locus of R.
View SolutionThe tangent at P(at2,2at) to the parabola y2=4ax intersects X axis at A and the normal at P meets it at B then area of triangle PAB is
View SolutionA tangent to the parabola y2=4bx=0 meets the parabola y2=4ax in P and Q. Then the locus of the middle points of PQ is:
View SolutionThe tangent and normal at the point P[at2,2at) to the parabola y2=4ax meet the x-axis in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle through T, P, G is
View Solution
