Let F(x) be an indefinite integral of sin2x
Statement-1: The function F(x) satisfies F(x+π)=F(x) for all real x. because
Statement-2: sin3(x+π)=sin2x for all real x.
A) Statement-1: True , statement-2 is true, Statement -2 is not a correct explanation for statement -1
c) Statement-1 is True, Statement -2 is False.
D) Statement-1 is False, Statement-2 is True.
Statement (1) is true and statement (2) is true and statement (2) is correct explanation for (1)
Statement (1) is true and statement (2) is true and statement (2) is NOT correct explanation for (1)
Statement (1) is true but (2) is false
Statement (1) is false but (2) is true
The correct Answer is:D
Step by step video, text & image solution for Let F(x) be an indefinite integral of sin^(2)x Statement-1: The function F(x) satisfies F(x+pi)=F(x) for all real x. because Statement-2: sin^(3)(x+pi)=sin^(2)x for all real x. A) Statement-1: True , statement-2 is true, Statement -2 is not a correct explanation for statement -1 c) Statement-1 is True, Statement -2 is False. D) Statement-1 is False, Statement-2 is True. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRATIONBook:MOTIONChapter:INDEFINITE INTEGRATIONExercise:EXERCISE - 4 (LEVEL - I)
Explore 10 Videos
- HYPERBOLABook:MOTIONChapter:HYPERBOLAExercise:EXERCISE-4 (Level-II)
Explore 17 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:MOTIONChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise -4 Level -II
Explore 7 Videos
Similar Questions
Let F(x) be an indefinite integral of sin2x.
Statement- 1: The function F(x) satisfies F(x+π)=F(x) for all real x.
Statement- 2: sin2(x+π)=sin2x for all real x.
(A) Statement I is true, Statement II is also true, Statement II is the correct explanation of Statement I.
(B)Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
(C) Statement I is true, Statement II is false.
(D) Statement I is false, Statement II is ture.
View SolutionConsider the function F(x)=∫x(x−1)(x2+1)dxStatement-1: F(x) is discontinuous at x=1 ,Statement-2: Integrand of F(x) is discontinuous at x=1 (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View Solution
Knowledge Check
Let F(x) be an indefinite integral of sin2x Statement I The function F(x) satisfies F(x+π)=F(x) for all real x. Because Statement II sin2(x+π)=sin2x, for all real x. (A) Statement I is true, Statement II is also true,
Statement II is the correct explanation of Statement I. (B)Statement I is true, Statement II is also true,
Statement II is not the correct explanation of Statement I. (C) Statement I is true, Statement II is false. (D) Statement I is false, Statement II is ture.AStatement I is true, Statement II is also true,
Statement II is the correct explanation of Statement I.BStatement I is true, Statement II is also true,
Statement II is not the correct explanation of Statement I.CStatement I is true, Statement II is false.DStatement I is false, Statement II is ture.
Statement-1: The function F(x)=∫sin2xdx satisfies F(x+π)=F(x),∀ξnR ,Statement-2: sin2(x+π)=sin2x (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionLet f: R R be a continuous function defined by f(x)=1ex+2e−x . Statement-1: f(c)=13, for some c∈R . Statement-2: 0<f(x)≤12√2, for all x∈R . (1) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation for Statement-1 (2) Statement-1 is true, Statement-2 is false (3) Statement-1 is false, Statement-2 is true (4) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation for Statement-1
View SolutionStatement-1: ∫sin−1xdx+∫sin−1√1−x2dx=π2x+cStatement-2: sin−1x+cos−1x=π2 (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: Yield of R-Br follows the order 1∘>2∘>3∘ in Hundsdicker reaction
Statement -2: Hundsdicker reaction follows free redical mechanism.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: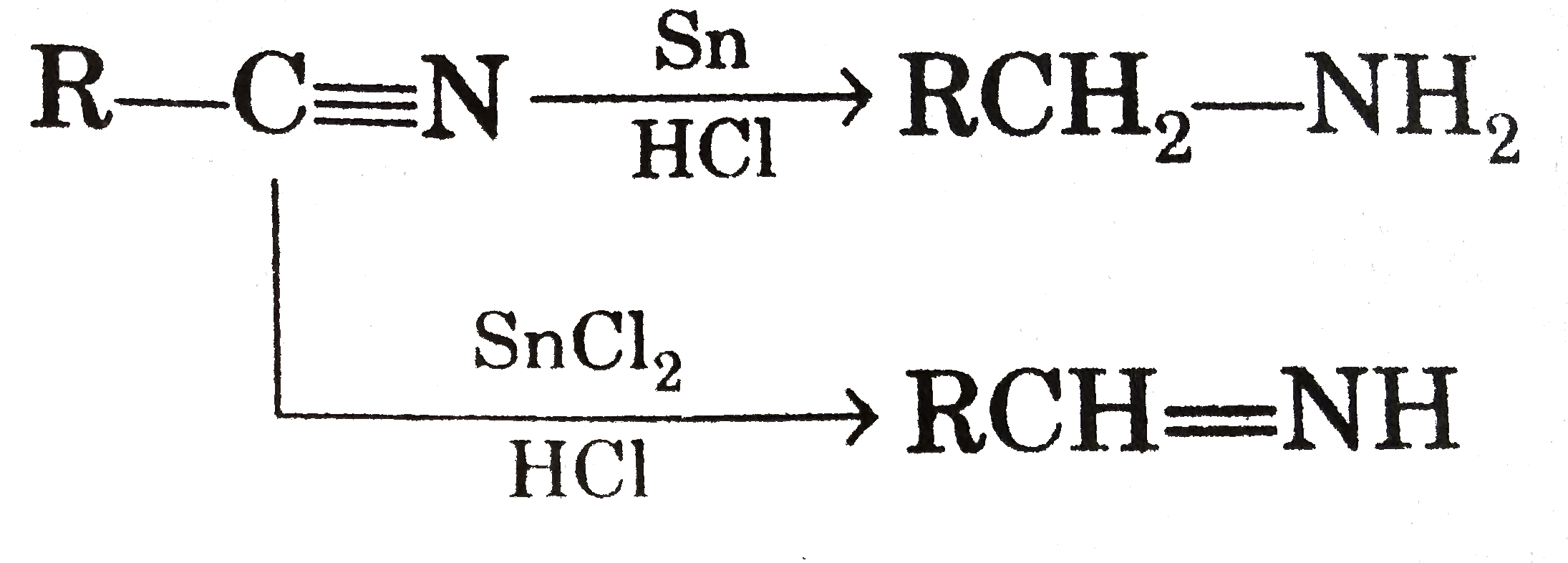
Statement-2: Sn can give maximum of 4 electron during reduction, whereas SnCl2 can give only 2.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: Effective molecular mass of acetic acid is 120.
Statement -2: It forms dimer due to intramolecular H-bonding.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: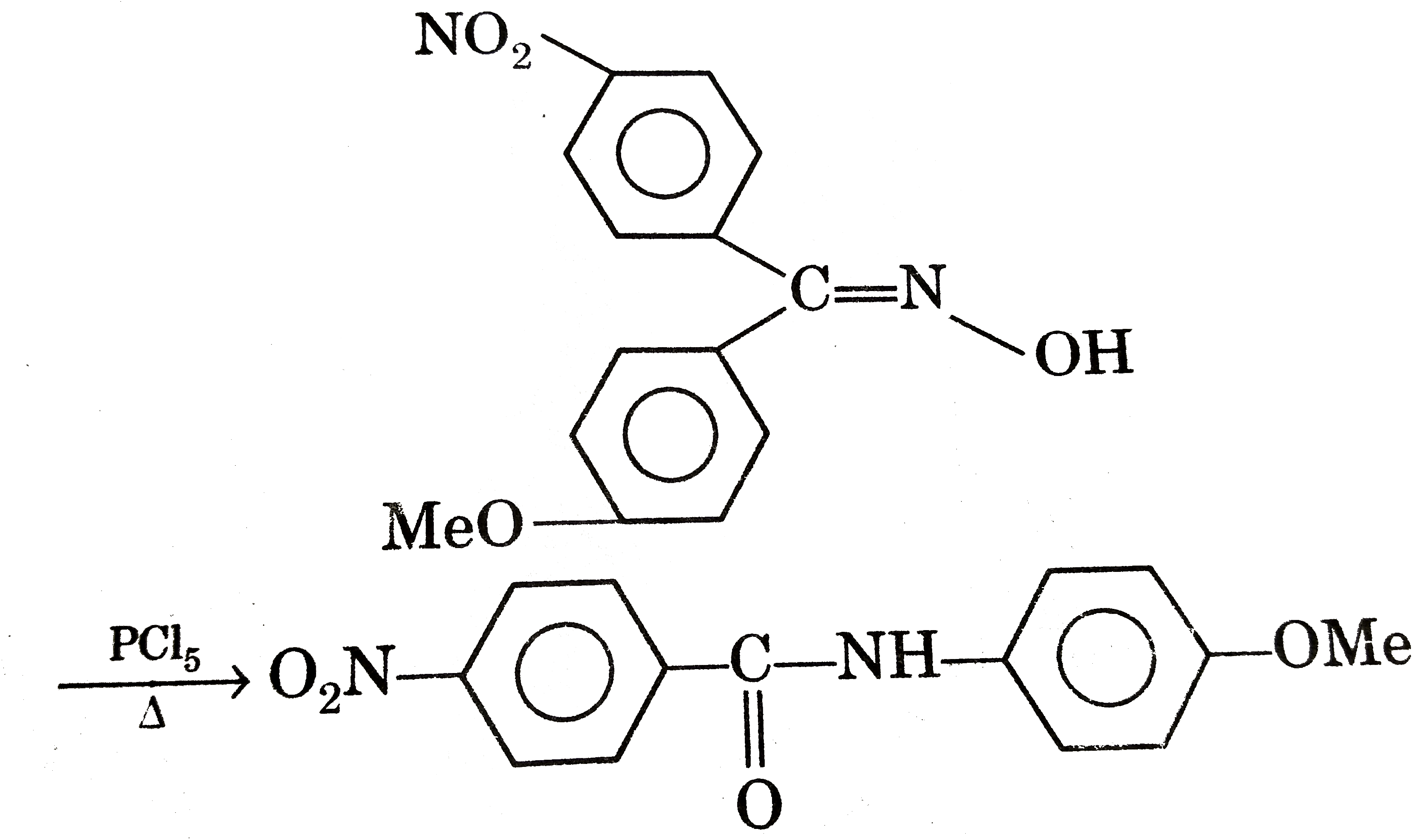
Statement -2: Migratory aptitude of p-methoxyphenyl group is greater than migratory aptitude p-nitrophenyl of group during carbrocation rearrangements.
View Solution

