For any real number x,let[x] denote the largest integer less than or equal to x,Letf be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x]isodd1+[x]−x,if[x]iseven Then the value of π210∫10−1f(x)cosπxdxis__
The correct Answer is:4
Step by step video, text & image solution for For any real number x ,l e t[x] denote the largest integer less than or equal to x ,L e tf be a real-valued function defined on the interval [-10 , 10] be f(x)={x-[x],if[x]i sod d1+[x]-x ,if[x]i se v e n Then the value of (pi^2)/(10)int_(-1)^(10)f(x)cospixdxi s____ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DEFINITE INTEGRATION Book:MOTIONChapter:DEFINITE INTEGRATION Exercise:EXERCISE -4 LEVEL-I
Explore 15 Videos
- CONTINUITY Book:MOTIONChapter:CONTINUITY Exercise:EXERCISE - 4 (LEVEL -II) (PREVIOUS YEAR JEE ADVANCED)
Explore 5 Videos
- DETERMINANTS Book:MOTIONChapter:DETERMINANTS Exercise:EXERCISE-4 (LEVEL-II)
Explore 6 Videos
Similar Questions
f(x)={x−[x],if[x]is odd1+[x]−x,if[x] is even
Then, the value of π210∫10−10f(x)cosπ×dx is
View SolutionFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
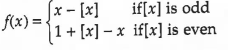 Then, the value of (π10)2(∫10−10f(x)cosπxdx is
Then, the value of (π10)2(∫10−10f(x)cosπxdx is
View Solution
Knowledge Check
For any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx isA2B4C0DNone of theseFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
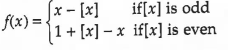 Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1
Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1For a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
AIf is differentiable on R.Bf is symmetric about the line x=0C∫3−3f(x)dx=0DFor each real α, the equation f(x)−α=0 has infinitely many roots.
For any real number x, let [x] denote the largest integer less than or equal to x. If
∫100[√10xx+1]dx then the value of 9I is
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let f: R→ R be defined as f(x)=2x+[x]+sinxcosx then f is
View SolutionFor a real number x, lel [x] denotes the griater + integer less than or equal to x. let f:R→R be defined by f(x)=2x+[x] then f is:
View SolutionFor a real number x let [x] denote the largest intger less than or equal to x. The smalleset positive integer n for which the integer ∫n1[x][√x]dx exceeds 60 is-
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x]. The possible integer value of n for which ∫n1[x]{x}dx exceeds 2013 is
View Solution

