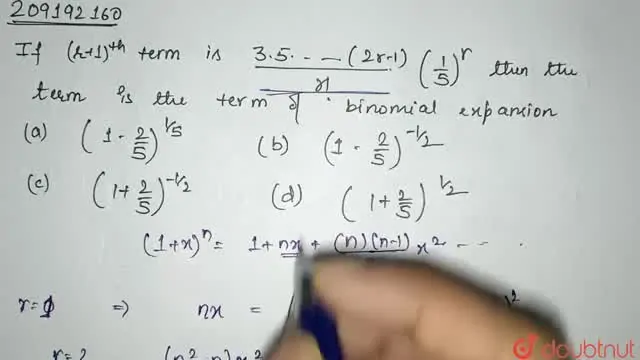If term is , then this is the term of binomial expansion-
The correct Answer is:B
Step by step video, text & image solution for If (r+1)^(th) term is (3.5...(2r-1))/(r!) (1/5)^(r), then this is the term of binomial expansion- by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - BINOMIAL THEOREM EXERCISE - Exercise - 2 (Level - II) (Multiple Correct ) (GENERAL TERM)2videos
BINOMIAL THEOREM
- BOOK - MOTIONCHAPTER - BINOMIAL THEOREM EXERCISE - Exercise - 2 (Level - II) (Multiple Correct ) (MIDDLE TERM )2videos
BINOMIAL THEOREM
- BOOK - MOTIONCHAPTER - BINOMIAL THEOREM EXERCISE - Exercise - 2 (Level - I) Objective Problems ( BINOMIAL THEOREM FOR ANY INDEX )4videos
BINOMIAL THEOREM
- BOOK - MOTIONCHAPTER - BASIC MATHEMATIC & LOGARITHM EXERCISE - Exercise - 44videos
BASIC MATHEMATIC & LOGARITHM
- BOOK - MOTIONCHAPTER - CIRCLEEXERCISE - Exercise - 4 | Level - II (Previous Year | JEE Advanced22videos
CIRCLE
Similar Questions
If rth term of a series is (2r+1)2−r then sum of its infinite terms is
View SolutionIf the rth term of a series is 1+x+x2+.......+xr−1 , then the sum of the first n terms is
View SolutionGiven positive integers r>1,n>2 and that the coefficient of (3rd)thand(r+2)th terms in the binomial expansion of (1+x)2n are equal. Then n=2r b. n=2r+1 c. n=3r d. none of these
View SolutionRatio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of (21/3+12(3)1/3)10 is
View Solution(r+1)th term in the expansion of (1−x)−4 will be
View SolutionThe ratio of the coefficient of terms (xn−rarandxran−r is the binomial expansion of (x+a)nwill be:
View SolutionIf (r+1)th term in the expasnion of (a33−2a2)10 contains a20 then the value of r is equal to
View SolutionIf rthterm in the expansion of (x3−2x2)10contains x4, then find the value of r
View SolutionIf rth term is the middle term in the expansion of (x2−12x)20, then (r+3)th term is
View SolutionIf the coefficients of the rth, (r +1)th and (r + 2)th terms in the binomial expansion of (1 + y)^(m) are in A.P., then m and r satisfy the equation
View Solution