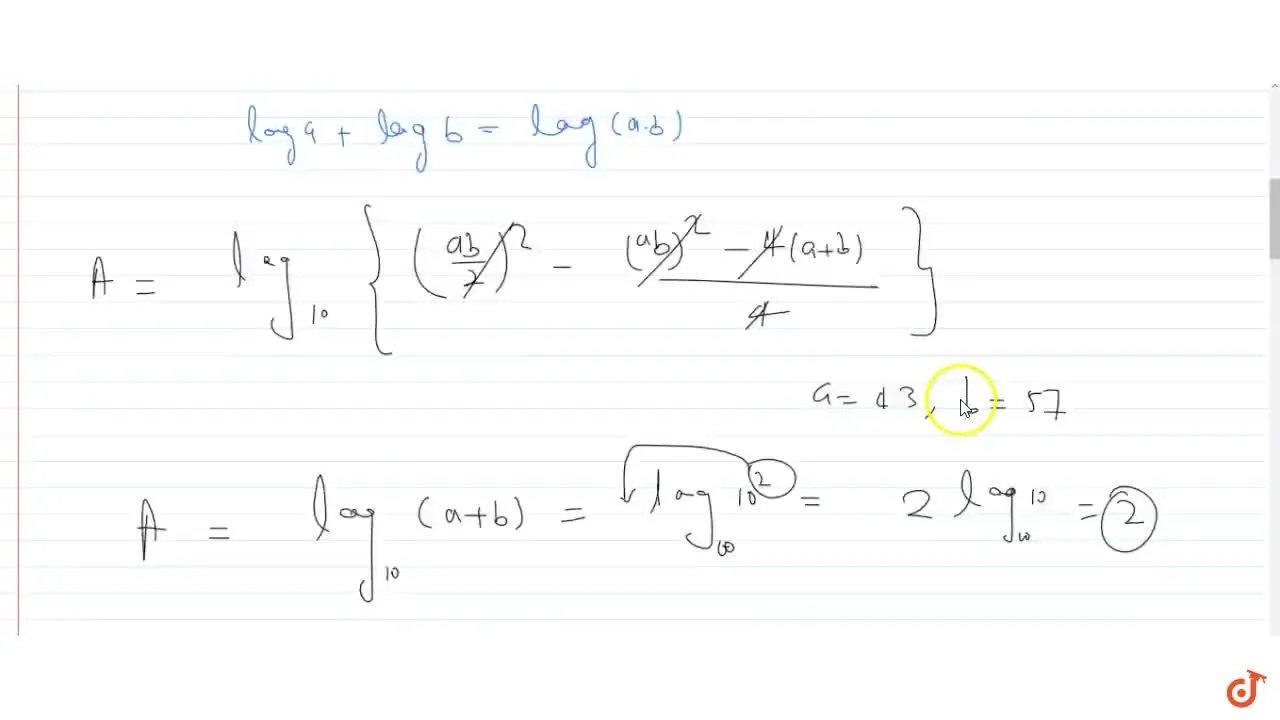Let A denotes the value of log10⎧⎪ ⎪⎨⎪ ⎪⎩ab+√(ab)2−4(a+b)2⎫⎪ ⎪⎬⎪ ⎪⎭+log10⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩log10(ab−√(ab)2−4(a+b))2⎫⎪ ⎪ ⎪ ⎪⎬⎪ ⎪ ⎪ ⎪⎭ and B denotes the value of the expression (2log618)⋅(3log63) Find the value of (A⋅B)
The correct Answer is:12
Step by step video, text & image solution for Let A denotes the value of log_10 {(ab+sqrt((ab)^2-4(a+b)))/2}+log_10 {log_10 (ab-sqrt((ab)^2-4(a+b)))/2} and B denotes the value of the expression (2^(log_6 18))*(3^(log_6 3)) Find the value of (A*B) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - BASIC MATHEMATIC & LOGARITHM EXERCISE - Exercise - 44videos
BASIC MATHEMATIC & LOGARITHM
- BOOK - MOTIONCHAPTER - BASIC MATHEMATIC & LOGARITHM EXERCISE - Exercise - 2 (Level -II)11videos
BASIC MATHEMATIC & LOGARITHM
- BOOK - MOTIONCHAPTER - AREA UNDER THE CURVEEXERCISE - EXERCISE - 4 LEVEL - II14videos
AREA UNDER THE CURVE
- BOOK - MOTIONCHAPTER - BINOMIAL THEOREM EXERCISE - Exercise -4 (Level - II) ( Previous Year )7videos
BINOMIAL THEOREM
Similar Questions
Let A denotes the value of log10⎧⎪ ⎪⎨⎪ ⎪⎩ab+√(ab)2−4(a+b)2⎫⎪ ⎪⎬⎪ ⎪⎭+log10⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩log10(ab−√(ab)2−4(a+b))2⎫⎪ ⎪ ⎪ ⎪⎬⎪ ⎪ ⎪ ⎪⎭ and B denotes the value of the expression (2log618)⋅(3log63) Find the value of (A⋅B)
View SolutionThe value of logab−log|b|=
View SolutionThe value of log10(bc)a2+log10(ac)b2+log10(ab)c2 is
View SolutionThe value of loga(x)logabx−logab
View SolutionThe value of loga(x)logabx−logab
View SolutionLet L denotes the value of a satisfying the equation log√3(a)=103 and M denotes the value of b satisfying the equation 4log39+9log42=10log83b. Find (L+M)
View SolutionWhat is the value of
12log1025−2log103+log1018?View Solution[log(a2bc)+log(b2ac)+log(c2ab)] is equal to 0 b. 1 c. 2 d. abc
View SolutionThe value of the expression 1log4(18)+12log6(3)+log6(2)+2log3(18)'is
View SolutionThe value of log(ab)2−log(ac)+log(bc4)−3log(bc) is:
View Solution