A cylindrical conductor has length $l$ and area of cross section A. Its conductivity changes with distance $(x)$ from one of its ends as $σ = σ_{0} \frac{l}{x} . [σ_{0} is a constant]$ . Calculate electric field inside the conductor as a function of $x$ , when a cell of emf V is connected across the ends.

$\frac{2 V x}{l^{2}}$

$\frac{3 \sqrt{l}}{3 A σ_{0}}$

$\frac{\sqrt{l}}{3 A σ_{0}}$

$\frac{4 \sqrt{l}}{3 A σ_{0}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A cylindrical conductor has length l and area of cross section A. Its conductivity changes with distance (x) from one of its ends as sigma = sigma_(0) (l)/(x). [sigma_(0) "is a constant"]. Calculate electric field inside the conductor as a function of x, when a cell of emf V is connected across the ends. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS NTA JEE MOCK TEST 22

Topper's Solved these Questions

Knowledge Check

A conductor of length l and area of cross-section A has a resistance R then its specific resistance is
A $ρ = \frac{R A}{l}$
B $ρ = R A l$
C $ρ = \frac{l}{R A}$
D $ρ = \frac{R^{2} A}{l}$
A cylindrical conductor of length l and uniform area of cross section A has resistance R. Another conductor of length 2.5l and resistance 0.5R of the same material has an area of cross section
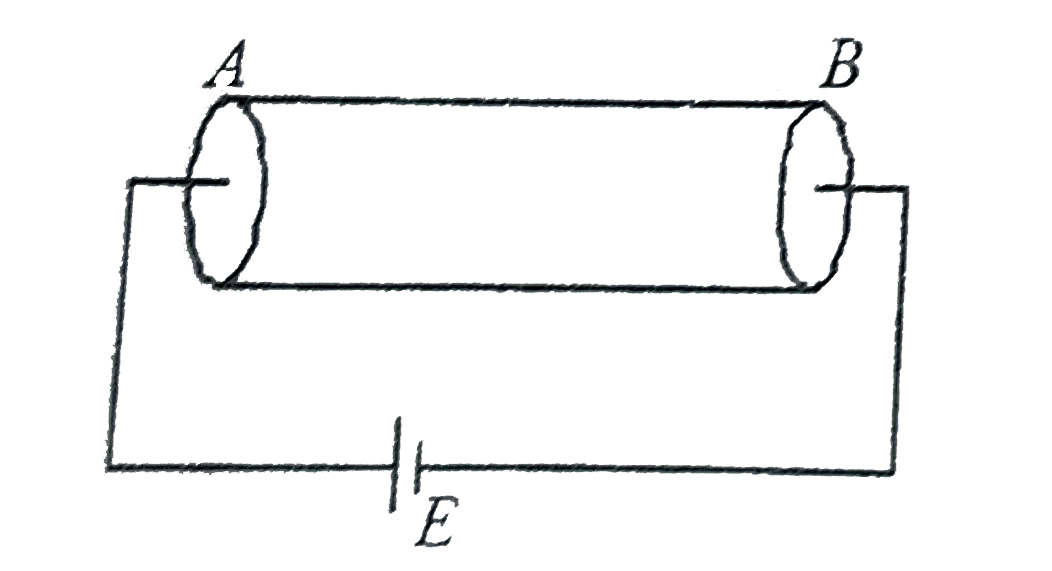
A5A
B2.5A
C0.5A
D $\frac{1}{5} A$
A cylindrical conductor AB of length l and area of cross-section a is connected to a battery having emf E and negligible internal resistance. The specific conductivity of cylindrical conductor varies as $σ = σ_{0} \frac{1}{\sqrt{x}}$ , where $σ_{0}$ is constant and x is distance from end A. What is the electric field just near the end B of cylinder?

A $\frac{E}{l}$
B $\frac{3 E}{2 l}$
C $\frac{2 E}{3 l}$
D $\frac{E}{2 l}$