Two particles of equal mass m are moving with velocities vˆi and v(ˆi+ˆj2) respectively. If the particles collide completely inelastically, then the energy lost in the process is
3mv24
2mv23
mv23
mv28
The correct Answer is:D
To solve the problem of two particles colliding completely inelastically, we will follow these steps:
Step 1: Define the initial velocities
Let the velocities of the two particles be:
- Particle 1: →v1=v^i
- Particle 2: →v2=v2^i+v2^j
Step 2: Calculate the initial momentum
The momentum of each particle can be calculated as follows:
- Momentum of Particle 1:
→p1=m→v1=mv^i
- Momentum of Particle 2:
→p2=m→v2=m(v2^i+v2^j)=mv2^i+mv2^j
Step 3: Calculate the total initial momentum
The total initial momentum →pinitial is the vector sum of the momenta of both particles:
→pinitial=→p1+→p2=mv^i+(mv2^i+mv2^j)=(mv+mv2)^i+mv2^j
→pinitial=3mv2^i+mv2^j
Step 4: Calculate the final velocity after collision
Since the collision is completely inelastic, the two particles stick together after the collision. The total mass after collision is 2m. The final momentum →pfinal is equal to the total initial momentum:
→pfinal=(2m)→vf
Setting the initial momentum equal to the final momentum:
3mv2^i+mv2^j=(2m)→vf
Dividing through by 2m:
→vf=3v4^i+v4^j
Step 5: Calculate the initial kinetic energy
The initial kinetic energy KEinitial is the sum of the kinetic energies of both particles:
KEinitial=12mv2+12m(v2)2+12m(v2)2
Calculating the second particle's kinetic energy:
KEinitial=12mv2+12m(v24)+12m(v24)=12mv2+14mv2=34mv2
Step 6: Calculate the final kinetic energy
The final kinetic energy KEfinal after the collision is:
KEfinal=12(2m)(3v4)2+12(2m)(v4)2
Calculating:
KEfinal=m(9v216+v216)=m(10v216)=58mv2
Step 7: Calculate the energy lost
The energy lost ΔKE during the collision is:
ΔKE=KEinitial−KEfinal
Substituting the values:
ΔKE=34mv2−58mv2
Finding a common denominator:
ΔKE=68mv2−58mv2=18mv2
Final Answer
The energy lost in the process is:
ΔKE=18mv2
Let the velocities of the two particles be:
- Particle 1: →v1=v^i
- Particle 2: →v2=v2^i+v2^j
The momentum of each particle can be calculated as follows:
- Momentum of Particle 1:
→p1=m→v1=mv^i
- Momentum of Particle 2:
→p2=m→v2=m(v2^i+v2^j)=mv2^i+mv2^j
The total initial momentum →pinitial is the vector sum of the momenta of both particles:
→pinitial=→p1+→p2=mv^i+(mv2^i+mv2^j)=(mv+mv2)^i+mv2^j
→pinitial=3mv2^i+mv2^j
Since the collision is completely inelastic, the two particles stick together after the collision. The total mass after collision is 2m. The final momentum →pfinal is equal to the total initial momentum:
→pfinal=(2m)→vf
Setting the initial momentum equal to the final momentum:
3mv2^i+mv2^j=(2m)→vf
Dividing through by 2m:
→vf=3v4^i+v4^j
The initial kinetic energy KEinitial is the sum of the kinetic energies of both particles:
KEinitial=12mv2+12m(v2)2+12m(v2)2
Calculating the second particle's kinetic energy:
KEinitial=12mv2+12m(v24)+12m(v24)=12mv2+14mv2=34mv2
The final kinetic energy KEfinal after the collision is:
KEfinal=12(2m)(3v4)2+12(2m)(v4)2
Calculating:
KEfinal=m(9v216+v216)=m(10v216)=58mv2
The energy lost ΔKE during the collision is:
ΔKE=KEinitial−KEfinal
Substituting the values:
ΔKE=34mv2−58mv2
Finding a common denominator:
ΔKE=68mv2−58mv2=18mv2
The energy lost in the process is:
ΔKE=18mv2
Topper's Solved these Questions
Similar Questions
Two particles of mass 2m and m moving with speed v and 2v respectively perpendicular to each other collides perfectly inelastically, then
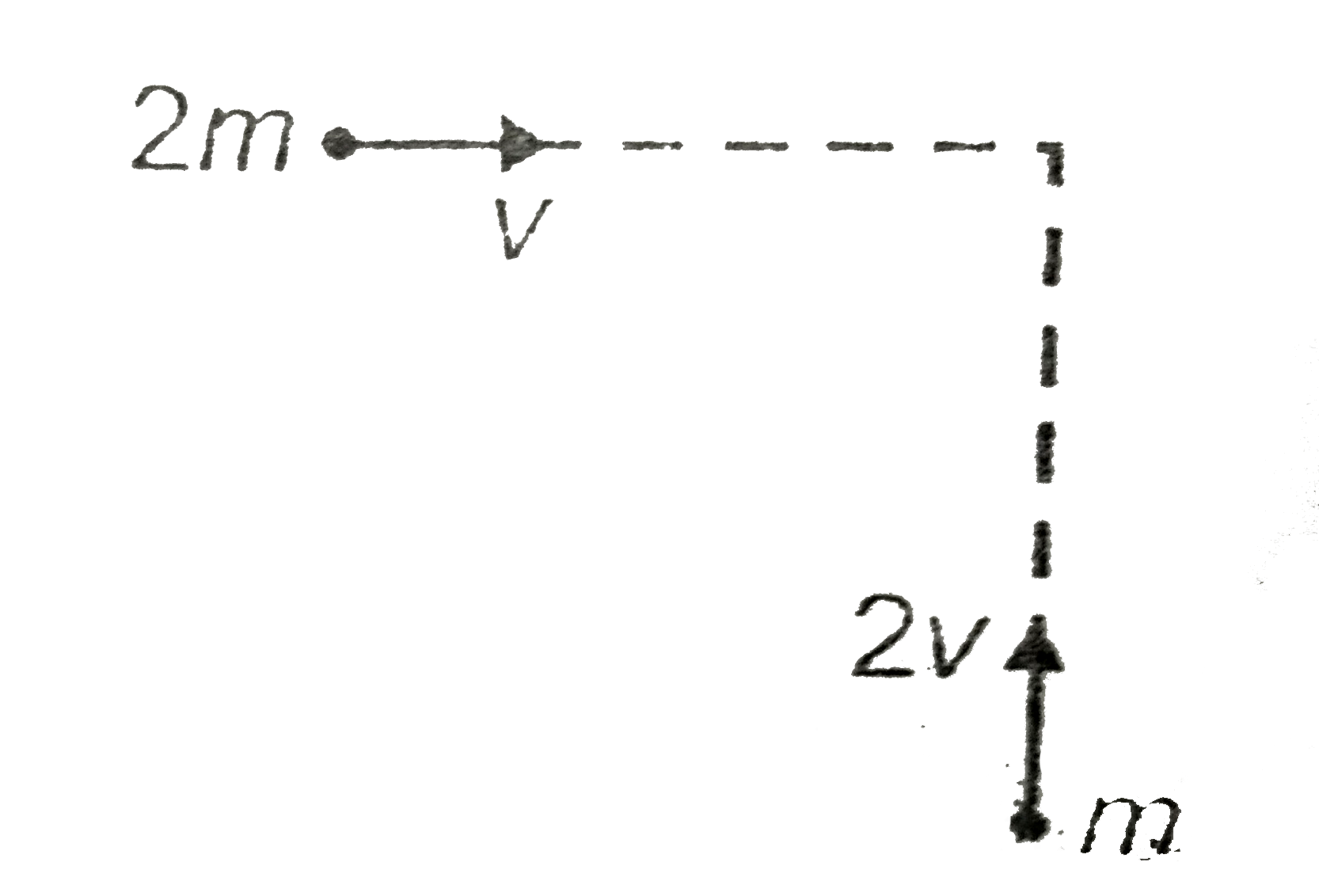
Loss in kinetic energy of the system
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View Solution
Knowledge Check
Two particles of mass m & 2m have velocities uˆj & uˆi respectively . They collide completely inelastically. Find the loss in kinetic energy of the system.
Amu2B23mu2Cmu24Dmu24Two particles of same mass 'm' moving with velocities →v1=vˆi,and→v2=(v2)ˆi+(v2)ˆjcollide in-elastically. Find the loss in kinetic energy
Amv28B5mv28Cmv24D3mv28Two particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
A1/2m(u1−u2)2B1/4m(u1−u2)2Cm(u1−u2)2D2m(u1−u2)2
Two particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Find the angle with the horizontal to which the particles move after collision.
View SolutionTwo particles are moving with velocities v1=ˆi+tˆj+ˆk and v2=tˆi+tˆj+2ˆkm/s respectively. Time at which they are moving perpendicular to each other is.____________(second)
View SolutionThree particles with masses 10, 20 and 40gm are moving with velocities 10ˆi,10ˆjand10ˆk m/sec respectively. If due to some interaction the first particle comes to rest and the velocity of second becomes )(3ˆi+4ˆj) m/sec. then the velocity of third particle after the interaction is-
View SolutionTwo particles of equal mass have velocities 2ˆims−1 and 2ˆjms−1. First particle has an acceleration (ˆi+ˆj)ms−2 while the acceleration of the second particle is zero. The centre of mass of the two particles moves in ?
View SolutionTwo particles of masses m and 2 m has initial velocity →u1=2ˆi+3ˆjms and →u2=−4ˆi+3ˆjms Respectivley. These particles have constant acceleration →a1=4ˆi+3ˆj(ms2) and →a2=−4ˆi−2ˆj(ms2) Respectively. Path of the centre of the centre of mass of this two particle system will be:
View Solution
