Calculate mean deviation about mean from the following data: xi: 3 9 17 23 27 fi: 8 10 12 9 5
5.09
6.09
7.09
8.09
The correct Answer is:C
To calculate the mean deviation about the mean from the given data, we will follow these steps:
Step 1: Create a table with xi and fi
We have the following data:
| xi | fi |
|---------|---------|
| 3 | 8 |
| 9 | 10 |
| 17 | 12 |
| 23 | 9 |
| 27 | 5 |
Step 2: Calculate fi⋅xi
Now, we will calculate the product of fi and xi for each row:
fi⋅xi for x1(3):3⋅8=24fi⋅xi for x2(9):9⋅10=90fi⋅xi for x3(17):17⋅12=204fi⋅xi for x4(23):23⋅9=207fi⋅xi for x5(27):27⋅5=135
Now, we will sum these products:
Σ(fi⋅xi)=24+90+204+207+135=660
Step 3: Calculate Σfi
Now, we will sum the frequencies fi:
Σfi=8+10+12+9+5=44
Step 4: Calculate the mean (¯x)
The mean ¯x is given by:
¯x=Σ(fi⋅xi)Σfi=66044=15
Step 5: Calculate the deviations |di|
Now we will calculate the deviations from the mean for each xi:
d1=3−15=−12d2=9−15=−6d3=17−15=2d4=23−15=8d5=27−15=12
Now, we take the absolute values:
|di|={12,6,2,8,12}
Step 6: Calculate fi⋅|di|
Now, we will calculate the product of fi and |di|:
f1⋅|d1|:8⋅12=96f2⋅|d2|:10⋅6=60f3⋅|d3|:12⋅2=24f4⋅|d4|:9⋅8=72f5⋅|d5|:5⋅12=60
Now, we will sum these products:
Σ(fi⋅|di|)=96+60+24+72+60=312
Step 7: Calculate the mean deviation
The mean deviation is given by:
Mean Deviation=Σ(fi⋅|di|)Σfi=31244≈7.09
Final Answer
The mean deviation about the mean is approximately 7.09.
---
|---------|---------|
| 3 | 8 |
| 9 | 10 |
| 17 | 12 |
| 23 | 9 |
| 27 | 5 |
Topper's Solved these Questions
Similar Questions
Calcualte the mean deviation about mean for the following data:

View SolutionCalculate the mean deviation about median for the following data:

View SolutionCalculate the mean deviation about median for the following data :
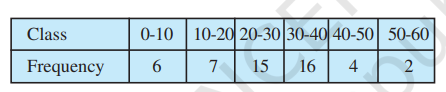
View SolutionCalculate the mean deviation about median for the following data:

View SolutionCalculate the mean deviation about median for the following data :
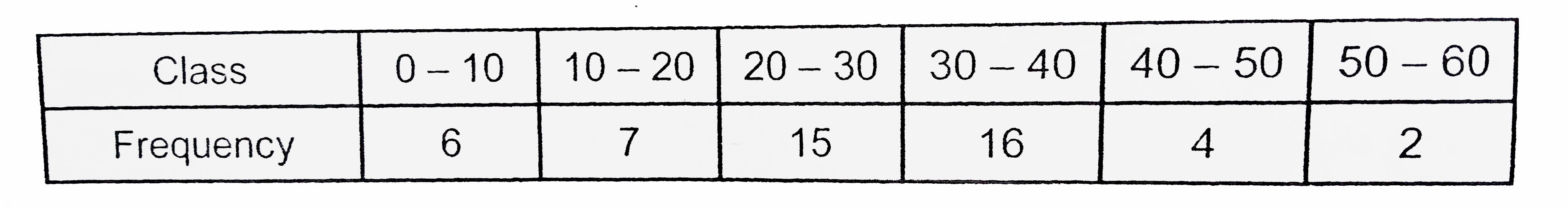
View SolutionFind the mean deviation about the mean for the following data :
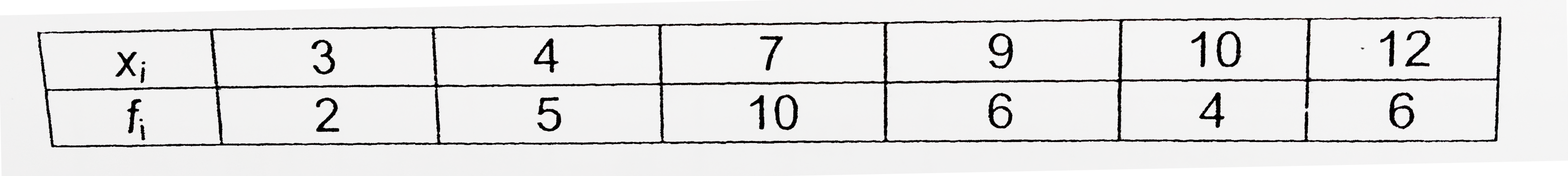
View SolutionFind the mean deviation about the mean for the following data :

View SolutionCalculate the mean deviation from the median of the following data:

View SolutionFind the mean deviation about the mean for the following data.

View SolutionCalculate mean and standard deviation from the following data:
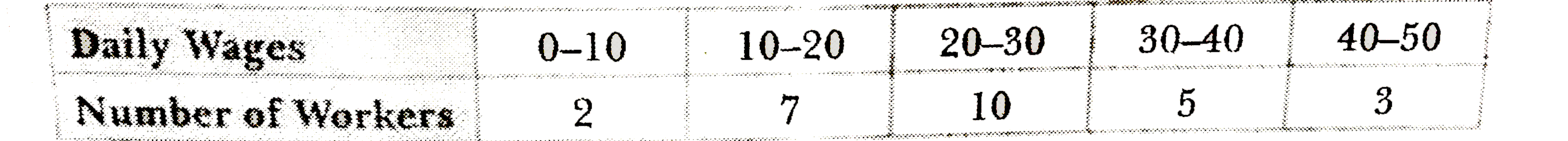
View Solution
