Let f = 50 Hz, and C = 100 μF in an AC circuit containing a capacitor only. If the peak value of the current in the circuit is 1.57 A at t = 0. The expression for the instantaneous voltage across the capacitor will be
C=50sin(100πt−π/2)
C=100sin(50πt)
C=50sin100πt
C=50sin(100πt+π/2)
The correct Answer is:A
To find the expression for the instantaneous voltage across the capacitor in the given AC circuit, we can follow these steps:
Step 1: Identify the given values
- Frequency (f) = 50 Hz
- Capacitance (C) = 100 µF = 100 × 10^(-6) F
- Peak current (I₀) = 1.57 A
Step 2: Calculate angular frequency (ω)
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×50=100π rad/s
Step 3: Calculate capacitive reactance (Xₐ)
The capacitive reactance (Xₐ) is given by:
XC=1ωC
Substituting the values of ω and C:
XC=1100π×100×10−6=10.01π=100π ohms
Step 4: Calculate peak voltage (V₀)
Using the relationship between peak current (I₀), peak voltage (V₀), and capacitive reactance (Xₐ):
I₀=V₀XC
Rearranging gives:
V₀=I₀×XC
Substituting the values:
V₀=1.57×100π
Calculating this gives:
V₀≈157π≈50 volts
Step 5: Write the expression for instantaneous voltage
In a purely capacitive circuit, the voltage lags the current by 90 degrees (or π/2 radians). Therefore, the instantaneous voltage (V(t)) can be expressed as:
V(t)=V₀sin(ωt−π2)
Substituting the values of V₀ and ω:
V(t)=50sin(100πt−π2)
Final Expression
Thus, the expression for the instantaneous voltage across the capacitor is:
V(t)=50sin(100πt−π2)
---
- Frequency (f) = 50 Hz
- Capacitance (C) = 100 µF = 100 × 10^(-6) F
- Peak current (I₀) = 1.57 A
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×50=100π rad/s
The capacitive reactance (Xₐ) is given by:
XC=1ωC
Substituting the values of ω and C:
XC=1100π×100×10−6=10.01π=100π ohms
Using the relationship between peak current (I₀), peak voltage (V₀), and capacitive reactance (Xₐ):
I₀=V₀XC
Rearranging gives:
V₀=I₀×XC
Substituting the values:
V₀=1.57×100π
Calculating this gives:
V₀≈157π≈50 volts
In a purely capacitive circuit, the voltage lags the current by 90 degrees (or π/2 radians). Therefore, the instantaneous voltage (V(t)) can be expressed as:
V(t)=V₀sin(ωt−π2)
Substituting the values of V₀ and ω:
V(t)=50sin(100πt−π2)
Thus, the expression for the instantaneous voltage across the capacitor is:
V(t)=50sin(100πt−π2)
Topper's Solved these Questions
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 2 (LEVEL - I)
Explore 19 Videos
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 2 (LEVEL - II)
Explore 5 Videos
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 4 (LEVEL - II)
Explore 14 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 4 (Level - II)
Explore 49 Videos
- ATOMIC STRUCTURE & X-RAY Book:MOTIONChapter:ATOMIC STRUCTURE & X-RAY Exercise:Exercise - 2
Explore 31 Videos
Similar Questions
Knowledge Check
In the circuit shown in figure, the final voltage drop across the capacitor C is :
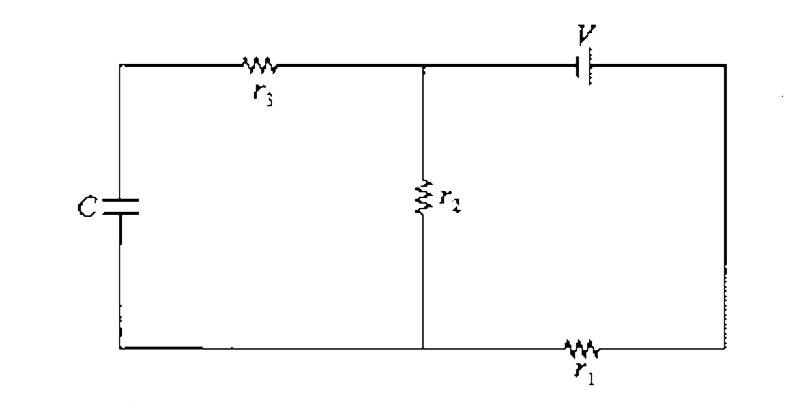 AVr1r1+r2BVr2r1+r2CV(r1+r2)r2DV(r2+r1)r1+r2+r3
AVr1r1+r2BVr2r1+r2CV(r1+r2)r2DV(r2+r1)r1+r2+r3A 30μF capacitor is connected to a 150 V, 60 Hz ac supply. The rms value of current in the circuit is
A17AB1.7AC1.7mAD2.7AA 40microF capacitor is connected to a 200V, 50 Hz ac supply. Rms value of current in circuit is nearly
A2.05AB2.5AC25.1AD1.7A
A capacitor of capacitance 12.0μF is joined to an AC source of frequency 200 Hz.The rms current in the circuit is 2.00 A. Find the rms voltage (in volt) across the capacitor.
View SolutionA 60 μF capacitor is connected to a 110 V, 60 Hz a.c. supply. Determine the rms value of the current in the circuit.
View SolutionA 3μF capacitor is connected to a 220 V, 50 Hz a.c. source. Calculate the rms value of current through the circuit. Also, find the peak value of voltage across the capacitor.
View SolutionIn ac circuit contains a pure capacitor, across which an ac emf
e=100sin(1000t), volt
is applied. If the peak value of the current is 200 mA, then the value of the capacitor is
View SolutionA capacitor of capacitance 2μF is connected in the tank circuit of an oscillator oscillating with a frequency of 1 kHz. If the current flowing in the circuit is 2mA, the voltage across the capacitor will be
View Solution

