A capacitor of capacitance 25μF is charged to 300V. It is then connected across a 10mH inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current 1.2ms after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at t=0 and t=1.2ms.
Charge across the capacitor at time t will be ,
q=q0cosωt
and i=−q0ωsinωt
Here q0=CV0=(25×10−6)(300)=7.5×10−3C
Now, charge is the capacitor after t=1.2×10−3s is,
q=(7.5×10−3)cos(2π×318.3)(1.2×10−3)C
=5.53×10−3C
∴ P.D. across capacitor,
V=|q|C=5.53×10−325×10−6=221.2 volt
The magnitude of current in the circuit at
t=1.2×10−3s is
|i|=q0ωsinωt
=(7.5×10−3)(2π)(318.3)sin(2π×318.3)(1.2×10−3)
A=10.13A
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 1
20 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 2 (LEVEL - I)
19 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - II)
49 Videos
- ATOMIC STRUCTURE & X-RAY BOOK - MOTIONCHAPTER - ATOMIC STRUCTURE & X-RAY EXERCISE - Exercise - 2
31 Videos
Similar Questions
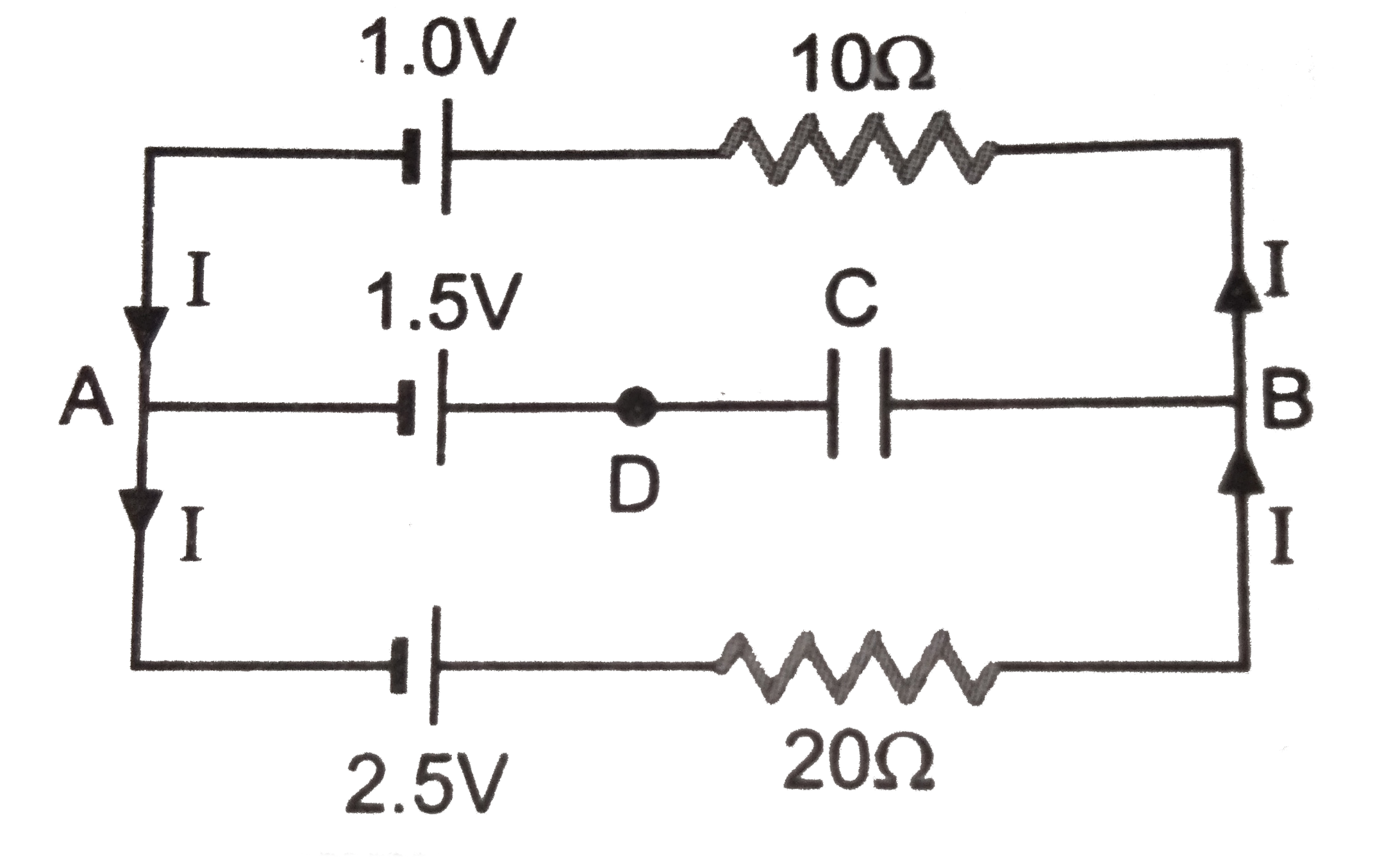
In the circuit diagram find the potential difference across the plates of capacitor C
View SolutionA capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. What is the current (in A) in the circuit at a time when the potential difference across the capacitor is 6.0V?
View Solution
Knowledge Check
A capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 0.2mH. At an instant when potential difference across the capacitor is 6v
Acurrent in the circuit is 1.04ABmagnetic energy in the magnetic field is 108μJCcurrent in the circuit is 1.04ADangular frequency of the circuit is 5×104radsIn the circuit shown, the potential difference across the 3μF capacitor is V and the equivalent capacitance between A and B is C Then:
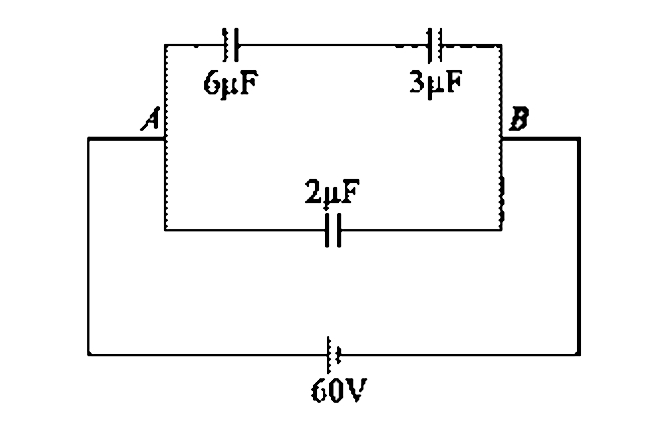 AC=4μFBC=11μFCV=20VDV=40V
AC=4μFBC=11μFCV=20VDV=40VIn the circuit shown in figure find

a. the equivalent capacitance
b. the charge stored in each capacitor and
c. the potential difference across each capacitor.A1.2μF 120μC 60Vand40VB1.2μF 120μC 60Vand20VC1.2μF 12μC 60Vand40VD12μF 120μC 60Vand40V
A capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA charged 10 micro farad capacitor is connected to a 81 mH inductor. What is the angular frequency of free oscillations of the circuit?
View SolutionA capacitor of capacitance 54μF is charged ot a potential of 25 V and then connected to a 15 mH inductor to produce oscillations. What was the energy stored in the capacitor initially and to what wavelength will the circuit respond ?
View SolutionIn the circuit shown the capacitors are C1=15μF,C2=10μFandC3=25μF. Find
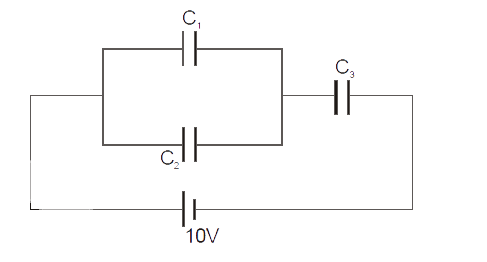
the potential difference across each capacitor.
View SolutionA charged 30 μF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit ?
View Solution
