In Fresnel’s birprism experiment, the two coherent sources are :
real
imaginary
one is real and other is imaginary
none of the above
The correct Answer is:B
Step by step video, text & image solution for In Fresnel’s birprism experiment, the two coherent sources are : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICS Book:MOTIONChapter:WAVE OPTICS Exercise:EXERCISE - 2 (Level - II) (Multiple Correct | JEE Advanced) Section A - Interference Problems + Wavefronts & Hugen’s Principle
Explore 1 Video
- WAVE OPTICS Book:MOTIONChapter:WAVE OPTICS Exercise:EXERCISE - 2 (Level - II) (Multiple Correct | JEE Advanced) Section B - YDSE Experiment
Explore 1 Video
- WAVE OPTICS Book:MOTIONChapter:WAVE OPTICS Exercise:EXERCISE - 2 (Level - I) (Objective Problems | JEE Main) Section B - YDSE Experiment
Explore 17 Videos
- WAVE MOTION Book:MOTIONChapter:WAVE MOTION Exercise:Exercise - 3 Section - B (Previous Years Problems)
Explore 7 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
In fresnel's biprism experiment the distance between the source and the screen is 1 ma nd that between the screen is 1 m and that between the source and biprism is 10 cm. the wavelength of light used is 6000Å. The fringe width obtained is 0.03 cm and the refracting angle of biprism is 1∘ then calculate the refractive index of the material of biprism.
View SolutionFigure shows a modified Fresnel biprism experiment with monochromatic source of wavelength 500 nm. The refracting angle of glass prism is 2∘. Find the fringe width.

View Solution
Knowledge Check
In Fresnel's biprims experiment coherent sources are obtained from an incoherent source using division of
AamplitudeBwavefrontCphaseeDnone of theseIn Fresnel's biprims experiment, the two sources of light are
Atwo virtual images of sliteBtwo real imatges of sliteCtwo independent of lightDnone of theseIn a Fresnel biprism experiment, the two positions of lens give separation between the slits as 16cm and 9cm respectively. What is the actual distance of separation?
A10.5 cmB12 cmC13 cmD14 cm
In Fresnel’s biprism experiment if the screen is moved away from the biprism, then the fringe width will :
View SolutionIn Fresnel's biprism experiment, the source contains two wavelength 6000 Å and 5000 Å. The fourth order bright fringe of first wavelength is at a distance of 3 mm from the central band. The distance of the same order of bright band of second wavelength from the central band is
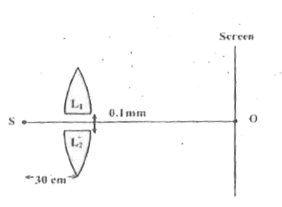
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
QDistance between the images Si and S2 will be
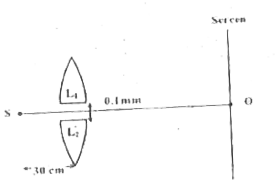
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Distance of a point from O, at which the sixth order minimum is formed, will be
View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Phase difference between the light waves 0.1 mm from along the screen, where intensity is half the maximum value, is

View Solution

