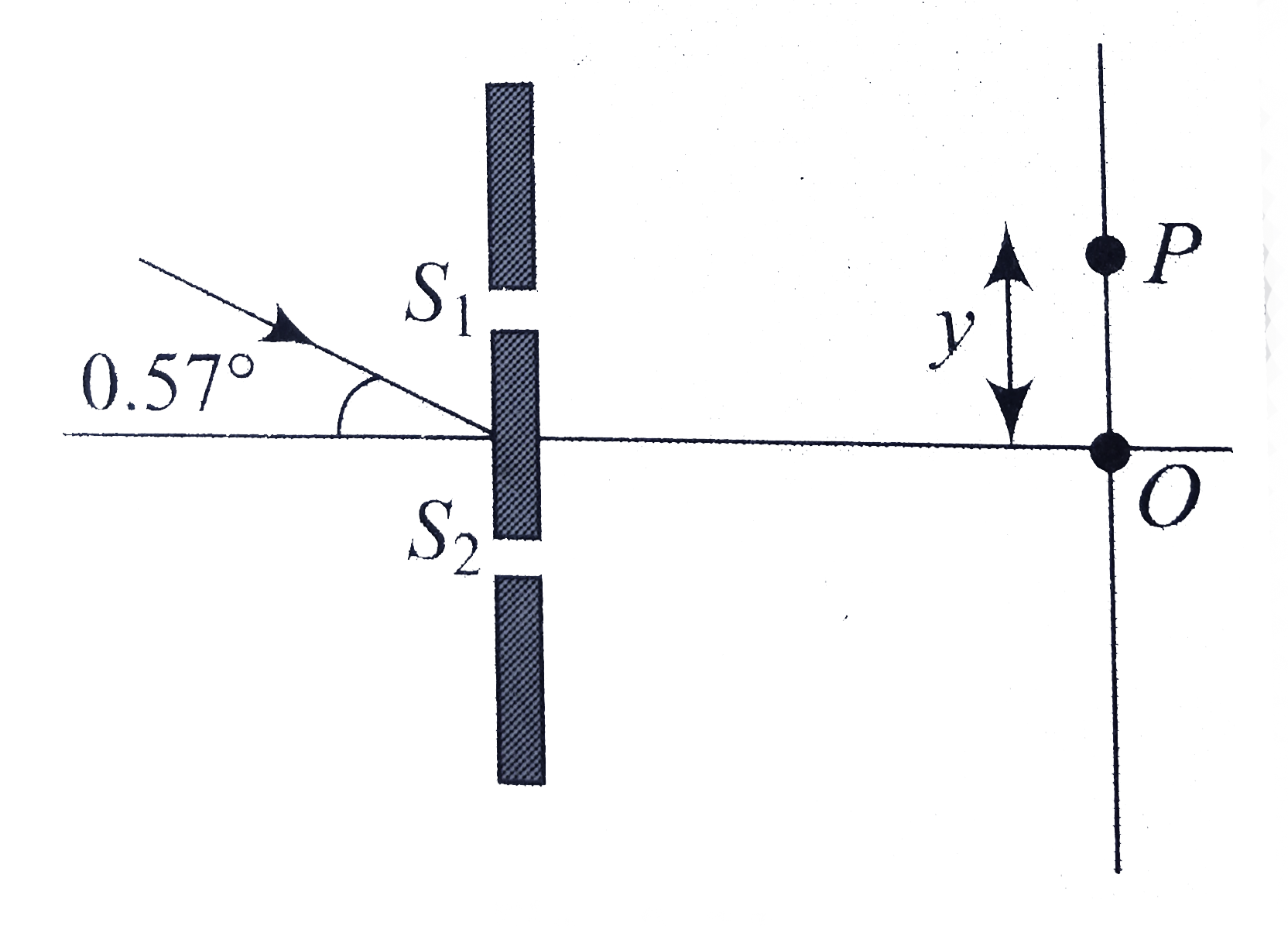
In YDSE with D = 1 m, d = 1 mm, light of wavelength 500 nm is incident

Light of wavelength 600 nm is incident normally on a slit of width 0.2 mm. The angular width of central maxima in the diffraction pattern is
A $6 \times 10^{- 3}$ rad
B $4 \times 10^{- 3}$ rad
C $2.4 \times 10^{- 3}$ rad
D $4.5 \times 10^{- 3}$ rad
The light of wavelength $6328 Å$ is incident on a slit of width $0.2 m m$ perpendicularly, the angular width of central maxima will be
A(a) ${0.36}^{\circ}$
B(b) ${0.18}^{\circ}$
C(c) ${0.72}^{\circ}$
D(d) ${0.09}^{\circ}$
In YDSE path difference at a point on screen is $\frac{λ}{8}$ . Find ratio of intensity at this point with maximum intensity.
A $0.853$
B $0.533$
C $0.234$
D $0.123$

$θ = θ_{0} = {0.57}^{\circ}$
$\Rightarrow y = - D tan θ ≅$
$- D θ = - 1 meter \times (\frac{0.57}{57} rad)$
$\Rightarrow y = - 1 c m$