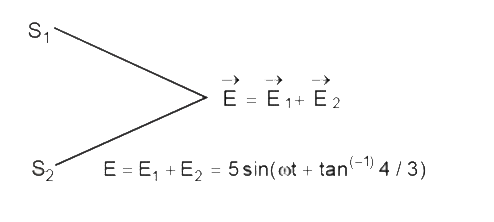$S_{1}$ and $S_{2}$ are two sources of light which produce individually disturbance at point $P$ given by $E_{1} = 3 sin ω t, E_{2} = 4 cos ω t .$ Assume $- \to E_{1} & {\to E}_{2}$ to along the same line, find the resultant after their superposition.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $5 sin (ω t + 53^{0})$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 1 (Objective Problems | JEE Main) Section A - Interference Problems + Wavefronts & Hugens Principle
9videos
WAVE OPTICS
BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 1 (Objective Problems | JEE Main) Section B - YDSE Experiment
8videos
WAVE OPTICS
BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)
7videos
WAVE MOTION
BOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)
10videos
WAVES

Similar Questions

Knowledge Check

Question 1 - Select One
In the given figure, if $i_{1} = 3 sin ω t and i_{2} = 4 cos t,$ then $i_{3}$ is

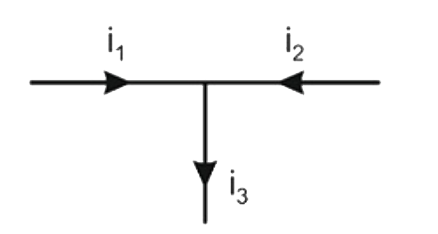A $5 sin (ω t + 53^{\circ})$
B $5 sin (ω t + 37^{\circ})$
C $5 sin (ω t + 45^{\circ})$
D $5 cos (ω t + 53^{\circ})$
Question 2 - Select One
The displacement of two interfering light waves are given by $y_{1} = 3 sin ω t, y_{2} = 4 sin (ω t + π / 2)$ . The amplitude of the resultant wave is
A3
B5
Czero
Done
Question 3 - Select One
Two waves $y_{1} = 2 sin ω t$ and $y_{2} = 4 sin (ω t + δ)$ superimpose. The ratio of the maximum to the minimum intensity of the resultant wave is
A9
B3
Cinfinity
DZero

MOTION-WAVE OPTICS -EXERCISE - 4 (Level - II) Previous Year | JEE Main

Home
Ask Doubt
Profile