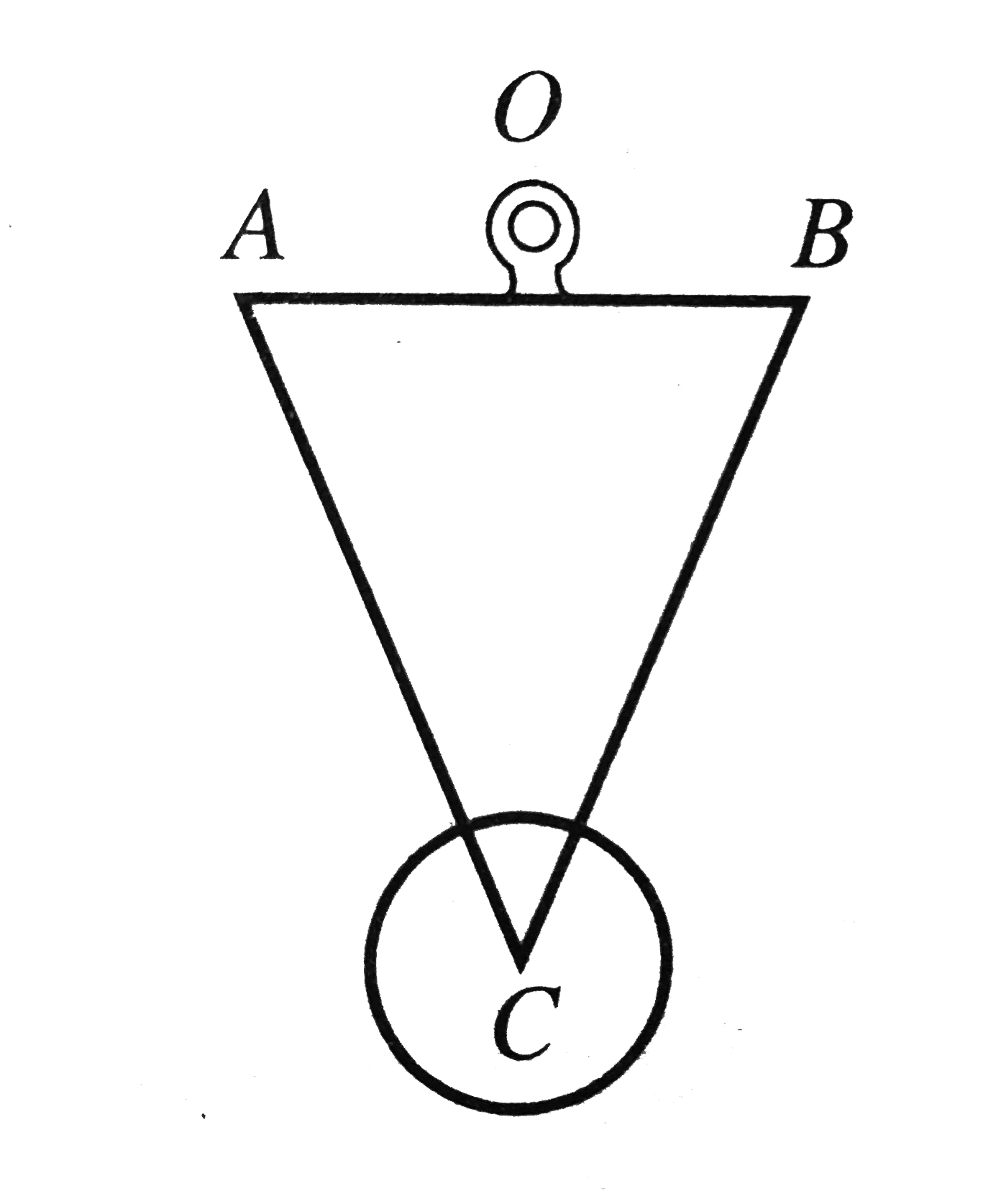
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length l1=5cm and coefficent of linar expansion α1=18×10−6 and side length l2 and coefficient of linear expansion α2=12×10−6. find l2 so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
l12√α1α2
Topper's Solved these Questions
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 4 (Level-I)
16 Videos
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 4 (Level-II)
11 Videos
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 3 (Level-II) (Section C - Youngs Modulus, Poissions Ratio)
1 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60 Videos
- Electrical Instrument BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -3
16 Videos
Similar Questions
In a compensated pendulum a triangular frame ABC is made using two different metals. AB of length l1 is made using a metal having coefficient of linear expansion α1. BC and AC of length l2 each have coefficient of linear expansion α2. A heavy bob is attached at C. Pendulum can oscillate about the pivot D. Find l2l1 so that distance of bob from the pivot point D does not change with change in temperature.
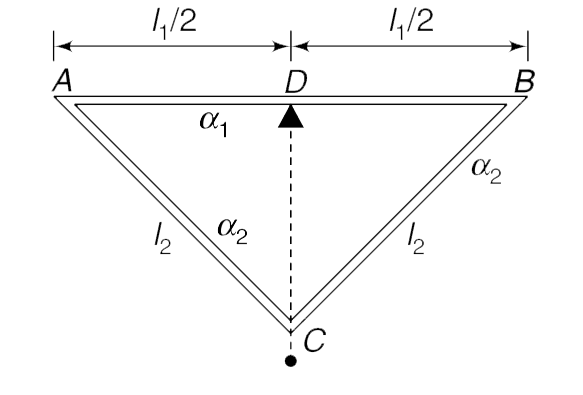
View SolutionThe compensated pendulum of a clock consista of an isosceles triangular frame of base length l1 and expansivity α1 and side length l2 and expansivity α2. The pendulum is supported as shown in the figure. Calculate the ratio l1/l2 so that the length of the pendulum may remain unchanged at all temperatures?
View Solution
Knowledge Check
A rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of theseA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of theseAn isosceles triangle is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is
 A2√α1α2B√α2α1C2√α2α1D12√α2α1
A2√α1α2B√α2α1C2√α2α1D12√α2α1
Among three rods, the first two are made of same material having coefficient of linear expansion α1 and the third rod is made of material of coefficient of linear expansion α2 . The third rod forms the base of the equilateral triangle when the three rods are arranged to form an equilateral triangle. If the altitude of triangle remains constant at all temperatures, what is the ratio of α1/α2 ?
View SolutionThere are two rods of length l1 l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionIf L1 and L2 are the lengths of two rods of coefficients of linear expansion α1 and α2 respectively the condition for the difference in lengths to be constant at all temperatures is
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View SolutionThe length of a brass rod is 1.5 m. Its coefficient of linear expansion is 19×10−6K−1 Find the increase in length of the rod if it is heated through 20∘C.
View Solution
