The earth receives solar radiation at a rate of $8.2 J c m^{- 2} - 1 min$ . Assuming that the sun radiates like a blackbody, Calculate the surface temperature of the sun. The angle subtended by the sun on the earth is ${0.55}^{\circ} C$ and the stefan constant $σ = 5.67 \times 10^{- s} W m^{- 2} K^{- 4}$ .

Video Solution

Text Solution

Verified by Experts

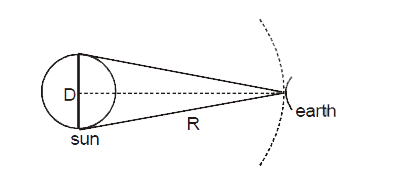
Let the diameter of the sun be D and its distance from the earth be R. From the questions
$\frac{D}{R} \approx 0.53 \times \frac{π}{180} = 9.25 \times 10^{- 3} \dots (i)$

The radiation emitted by the surface of the sun per unit time is
$4 π {(\frac{D}{2})}^{2} σ T^{4} = π D^{2} σ T^{4}$
At distance R, this radiation falls on an area $4 π R^{2}$ in unit time. the radiation received at the earth's surface per unit time per unit area is, therefore,
$\frac{π D^{2} σ T^{4}}{3 π R^{2}} = \frac{σ T^{4}}{4} {(\frac{D}{R})}^{2}$
Thus, $σ T^{4} \frac{)}{4} {(\frac{D}{R})}^{2} = 8.2 J / c m^{2} -$ minute
or, $\frac{1}{4} \times (5.67 \times 10^{- 8} \frac{W}{m^{2} - K^{4}}) T^{4} \times {(9.25 \times 10^{- 3})}^{2}$
$= \frac{8.2}{10^{- 4} \times 60 m^{2}}$
or, $T = 5794 K \approx 5800 K$ .

Updated on:21/07/2023

Calculate the temperature at which a perfect black body radiates at the rate of $1 W c m^{- 2}$ , value of Stefan's constant,
$σ = 5.67 \times 10^{- 8} W m^{- 2} K^{- 4}$
A576 K
B648 K
C695 K
D766 K
Calculate the temperature at which a perfect black body radiates at the rate of $1 W c m^{- 2}$ , value of Stefan's constant,
$σ = 5.67 \times 10^{- 5} W m^{- 2} K^{- 8}$
A $576 K$
B $648 K$
C $695 K$
D $766 K$
The solar constant for the earth is $\sum$ . The surface temperature of the sun is $T K$ . The sum subtends an angle $θ$ at the earth :-
A $\sum \propto T^{4}$
B $\sum \propto T^{2}$
C $\sum \propto θ^{2}$
D $\sum \propto θ$