Part of a simple harmonic motion is graphed in the figure, where $y$ is the displacement from the mean position. The correct equation describing this $S . H . M$ is-

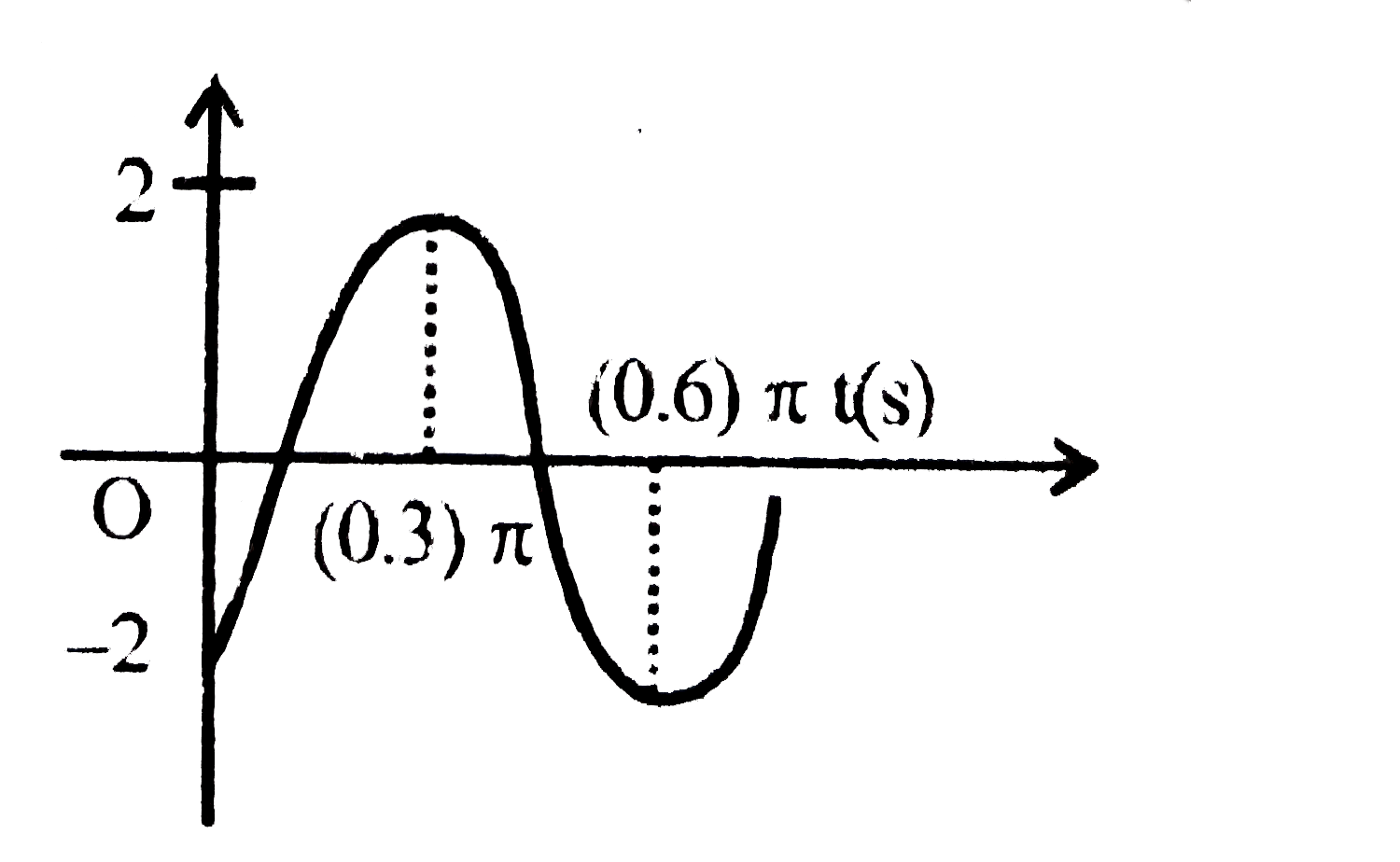
y =4 cos ( 0.6t)

$y = 2 sin (\frac{10}{3} t - \frac{π}{2})$

$y = 4 sin (\frac{10}{3} t + \frac{π}{2})$

$y = 2 cos (\frac{10}{3} t + \frac{π}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video & image solution for Part of a simple harmonic motion is graphed in the figure, where y is the displacement from the mean position. The correct equation describing this S.H.M is- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARONIC MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Part of SHM is graphed in the figure. Here, $y$ is displacement from mean position. The correct equation describing the SHM is

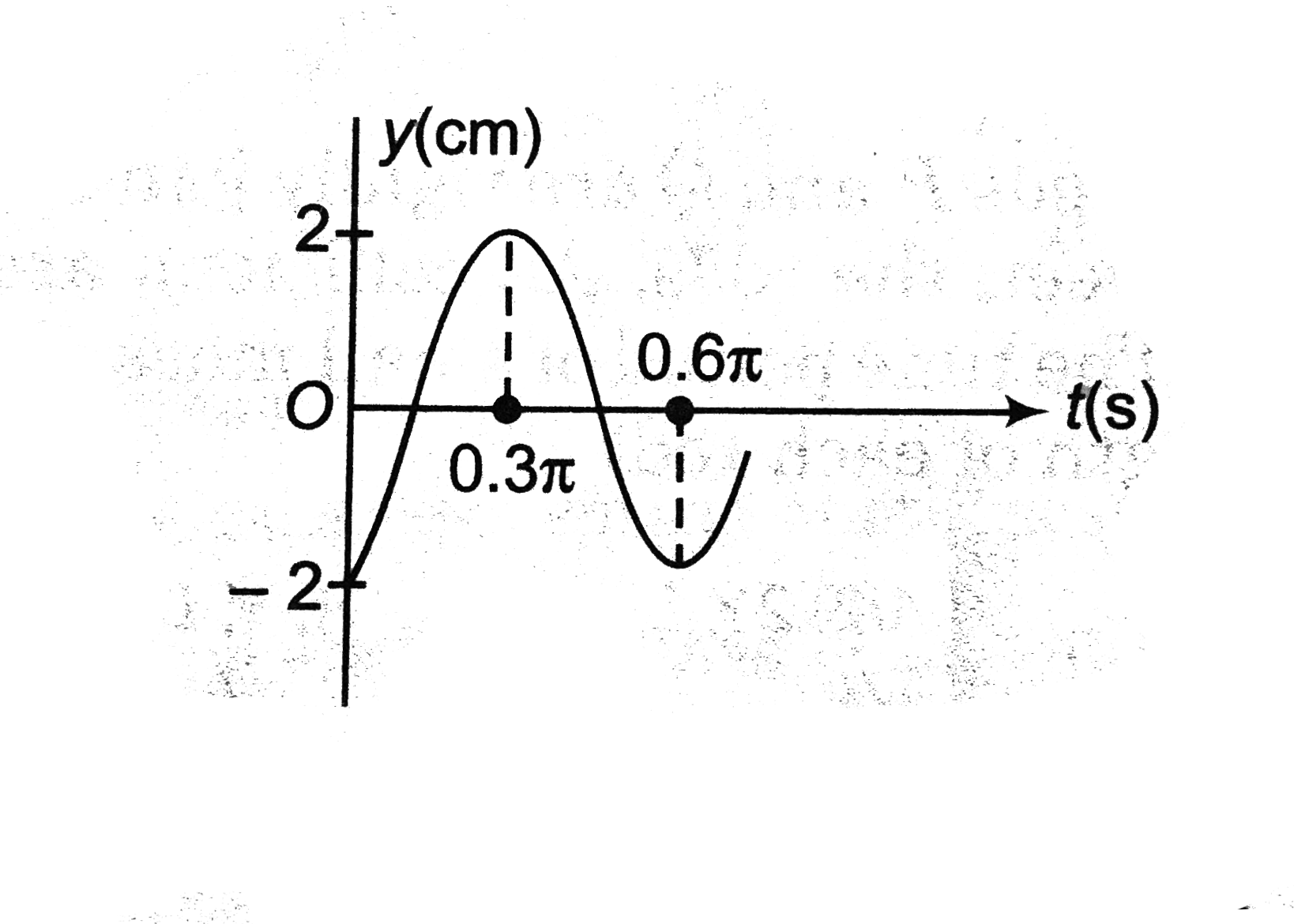A $y = 4 cos (0.6 t)$
B $y = 2 sin (\frac{10}{3} t - \frac{π}{2})$
C $y = 2 sin (\frac{π}{2} - \frac{10}{3} t)$
D $y = 2 cos (0.6 t + \frac{π}{2})$
Question 2 - Select One
The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
A(a) independent of x.
B(b) $\propto x^{2}$
C(c ) prop x
D(d) propx^(1//2)
Question 3 - Select One
The acceleration of a simple harmonic oscillator is $1 m / s^{2}$ when its displacement from mean position is 0.5 m. Then its frequency of oscillation is
A $\sqrt{2} π H z$
B $π / \sqrt{2} H z$
C $\frac{1}{\sqrt{2} π} H z$
D $\frac{\sqrt{2}}{π} H z$

MOTION-SIMPLE HARONIC MOTION -EXERCISE -2 (Leve-I) ( SECTION - A ) ( Equation of SHM, Velocity andAcceleration in SHM, Energy of SHM)

Home
Ask Doubt
Profile

Part of a simple harmonic motion is graphed in the figure, where y is the displacement from the mean position. The correct equation describing this S.H.M is-

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Part of SHM is graphed in the figure. Here, y is displacement from mean position. The correct equation describing the SHM is

The total energy of a particle, executing simple harmonic motion is. where x is the displacement from the mean position, hence total energy is independent of x.

The acceleration of a simple harmonic oscillator is 1m/s2 when its displacement from mean position is 0.5 m. Then its frequency of oscillation is

MOTION-SIMPLE HARONIC MOTION -EXERCISE -2 (Leve-I) ( SECTION - A ) ( Equation of SHM, Velocity andAcceleration in SHM, Energy of SHM)

Part of a simple harmonic motion is graphed in the figure, where $y$ is the displacement from the mean position. The correct equation describing this $S . H . M$ is-

Part of SHM is graphed in the figure. Here, $y$ is displacement from mean position. The correct equation describing the SHM is

The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.

The acceleration of a simple harmonic oscillator is $1 m / s^{2}$ when its displacement from mean position is 0.5 m. Then its frequency of oscillation is