x1=5sin(ωt+30∘), x2 = 10 cos (ωt) Find amplitude of resultant SHM.
Video Solution
Text Solution
x1=5sin(ωt+30∘)
x2=10sin(ωt+π2)
A=√52+102+2×5×10cos60∘
= √25+100+50=√175=5√7
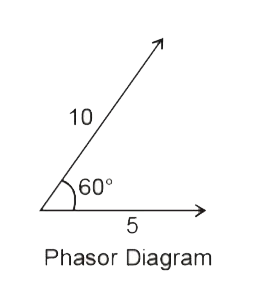
|
Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-A )
Explore 8 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
Knowledge Check
The displacements of two intering lightwaves are y1=4sinωt and y2=3cos(ωt). The amplitude of the resultant wave is (y1 and y2 are in CGS system)
A5 cmB7 cmC1 cmDzeroTwo waves are represented by y1=asin(ωt+π6)andy2=acosωt. What will be their resultant amplitude
AaB√2aC√3aD2aTwo waves having equaitons
x1=asin(ωt+ϕ1),x=asin(ω+ϕ2)
If in the resultant wave the frequency and amplitude remain equal to those of superimposing waves. Then phase difference between them isAπ6B2π3Cπ4Dπ3
x1=3sinωt,x2=4cos'ωt Find (i) amplitude of resultant SHM. (ii) equation of the resultant SHM.
View Solutionx1=3sinωt,x_(2) = 4 cos omega t
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View Solutionx1=3sinωt⇒x2=4cosωt. Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.
View SolutionThree light waves combine at a certain point where thcir electric field components are
E1=E0sinωt,
E2=E0sin(ωt+60∘),
E3=E0sin(ωt−30∘).
Find their resultant component E(t) at that point.
View SolutionA point participates simultaneously in two harmonic oscillations of the same direction:x1=acosωt and x2=acos2ωt. Find the maximum velocity of the point .
View Solution

